练习册

  • 练习册
  • 试题
    相关习题
     0  58609  58617  58623  58627  58633  58635  58639  58645  58647  58653  58659  58663  58665  58669  58675  58677  58683  58687  58689  58693  58695  58699  58701  58703  58704  58705  58707  58708  58709  58711  58713  58717  58719  58723  58725  58729  58735  58737  58743  58747  58749  58753  58759  58765  58767  58773  58777  58779  58785  58789  58795  58803  266669 

    科目： 来源： 题型：

    设数集M={x|m≤x≤m+},N={x|n≤x≤n},且M,N都是集合{x|0≤x≤1}的子集,如果把b-a叫做集合{x|a≤x≤b}的“长度”,那么集合M∩N的“长度”的最小值是

    A.                B.                C.                D.

    查看答案和解析>>

    科目： 来源： 题型：

    在边长为1的正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个由四个三角形围成的“四面体”,使G1,G2,G3三点重合,重合后的点记为G(如图),那么四面体S—EFG外接球的半径是

    A.              B.              C.              D.以上都不对

    查看答案和解析>>

    科目： 来源： 题型：

    设a、b是平面α外的任意两条线段,则“a、b相等”是“它们在α内的射影相等”的

    A.充分不必要条件                        B.必要不充分条件

    C.充分必要条件                          D.非充分又非必要条件

    查看答案和解析>>

    科目： 来源： 题型：

    设函数y=f(x)的定义域为R,f(0)=1,对于任意的实数m,n恒有f(m+n)=f(m)·f(n),且当x＞0时,0＜f(x)＜1,f(x)在R上的单调性是

    A.f(x)在R上是减函数                    B.f(x)在R上是增函数

    C.f(x)在R上是奇函数                    D.f(x)在R上是偶函数

    查看答案和解析>>

    科目： 来源： 题型：

    设复数z=+(1+i)2,则(1+z)7展开式的第五项是

    A.-21               B.35               C.-21i               D.-35i

    查看答案和解析>>

    科目： 来源： 题型：

    设x1、x2是函数f(x)=x3+x2-a2x(其中a＞0)的两个极值点,且|x1|+|x2|=2.

    (1)求a的取值范围;

    (2)设g(a)=eka(k∈R),求g(a)的单调区间;

    (3)若函数h(x)=f′(x)-2a(x-x1),求证:当x1＜x＜2且x1＜0时,有|h(x)|≤4a.

    查看答案和解析>>

    科目： 来源： 题型：

    已知圆C:(x-1)2+y2=r2(r＞1),设M为圆C与x轴负半轴的交点,过点M作圆C的弦MN,并使它的中点P恰好落在y轴上.

    (1)当r=2时,求满足条件的P点的坐标;

    (2)当r∈(1,+∞)时,求点N的轨迹E的方程;

    (3)若A(x1,2)、B(x2,y2)、C(x0,y0)是E上不同的点,且AB⊥BC,求y0的取值范围.

    查看答案和解析>>

    科目： 来源： 题型：

    已知数列{an}满足an=2an-1+2n+2(n≥2),a1=2.

    (1)求a2,a3,a4;

    (2)是否存在一个实数λ,使得数列{}成等差数列,若存在,求出λ的值;若不存在,请说明理由;

    (3)设Sn为数列{an}的前n项和,证明Sn＞n3+n2.

    查看答案和解析>>

    科目： 来源： 题型：

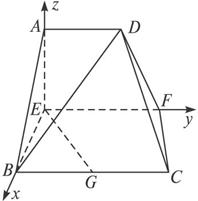
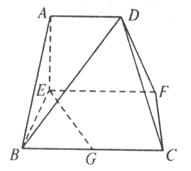
    已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=,AB=BC=2AD=4,E、F分别是AB、CD的中点,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF(如图).

        

    (1)求证:BD⊥EG;

    (2)求EG和平面ABCD所成的角;

    (3)求二面角B-DC-F的余弦值.

    查看答案和解析>>

    科目： 来源： 题型：

    某休闲会馆拟举行“五一”庆祝活动,每位来宾交30元的入场费,可参加一次抽奖活动.抽奖活动规则是:从一个装有分值分别为1,2,3,4,5,6的六个相同小球的抽奖箱中,有放回地抽取两次,每次抽取一个球,规定:若抽得两球的分值和为12分,则获得价值为m元的礼品;若抽得两球的分值和为11分或10分,则获得价值为100元的礼品;若抽得两球的分值和低于10分,则不获奖.

    (1)求每位会员获奖的概率;

    (2)假设会馆这次活动打算既不赔钱也不赚钱,则m应为多少元？

    查看答案和解析>>

    同步练习册答案