练习册

  • 练习册
  • 试题
    相关习题
     0  58631  58639  58645  58649  58655  58657  58661  58667  58669  58675  58681  58685  58687  58691  58697  58699  58705  58709  58711  58715  58717  58721  58723  58725  58726  58727  58729  58730  58731  58733  58735  58739  58741  58745  58747  58751  58757  58759  58765  58769  58771  58775  58781  58787  58789  58795  58799  58801  58807  58811  58817  58825  266669 

    科目： 来源： 题型：

    在三棱锥P—ABC中,D为底面ABC的边AB上一点,M为底面ABC内一点,且满足=,=+,则三棱锥P—AMD与三棱锥P—ABC的体积比为

    A.               B.               C.               D.

    查看答案和解析>>

    科目： 来源： 题型：

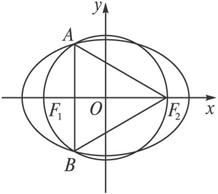
    如图,F1和F2分别是椭圆+=1(a＞b＞0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为

    A.               B.               C.               D.-1

    查看答案和解析>>

    科目： 来源： 题型：

    已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:小时)的函数,记为y=f(t),下表是某日各时的浪高数据.

    ｔ时

    0

    3

    6

    9

    12

    15

    18

    21

    24

    ｙ米

    1.5

    1.0

    0.49

    0.98

    1.49

    1.01

    0.5

    0.99

    1.5

    经长期观察,y=f(t)的曲线可以近似地看成是函数y=Acosωt+k的曲线,为安全起见,浴场规定:当浪高低于1米时才对冲浪爱好者开放,根据以上数据,当天在上午8:00时至晚上20:00时之间可供冲浪爱好者冲浪的时间约为

    A.4小时                B.5小时                 C.6小时                 D.8小时

    查看答案和解析>>

    科目： 来源： 题型：

    某电信公司推出手机两种收费方式:A种方式是月租20元,B种方式是月租0元.一个月的本地网内打出电话时间(分钟)与打出电话费s(元)的函数关系如图,当打出电话150分钟时,这两种方式电话费相差

    A.10元                 B.20元                 C.30元                 D.元

    查看答案和解析>>

    科目： 来源： 题型：

    已知函数f(x)=的定义域为M,g(x)=的定义域为N,则M∩N为

    A.(-1,3］                                       B.(-1,1)∪(1,3］

    C.［3,+∞)                                      D.(-1,1)∪(1,2］

    查看答案和解析>>

    科目： 来源： 题型：

    某篮球学校的甲乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如右,则甲乙命中个数的中位数分别为

    A.22,20                  B.24,18               C.23,19                  D.23,20

    查看答案和解析>>

    科目： 来源： 题型：

    已知向量a=(tanα,1),b=(,1),α∈(0,π),且a∥b,则α的值为

    A.或               B.                C.或               D.

    查看答案和解析>>

    科目： 来源： 题型：

    “ab＞0”是“复数a+bi(a,b∈R)对应的点在第一象限”的

    A.充分不必要条件                                B.必要不充分条件

    C.充要条件                                      D.既不充分也不必要条件

    查看答案和解析>>

    科目： 来源： 题型：

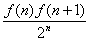    设不等式组所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)的个数为f(n)(n∈N*).

    (1)求f(1),f(2)的值及f(n)的表达式.(可以不作证明)

    (2)记Tn=,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围.

    (3)求证:当n∈N*时,++…+＜.

    查看答案和解析>>

    科目： 来源： 题型：

    函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.

    (1)求函数g(x)的解析式;

    (2)解不等式g(x)≥f(x)-|x-1|;

    (3)若h(x)=g(x)-λf(x)+1在［-1,1］上是增函数,求实数λ的取值范围.

    查看答案和解析>>

    同步练习册答案