有下列命题：①函数的周期为②已知数列的前n项和为S_n，若a₁=1且a_n+1=S_n+1，则数列为等比数列；③函数的图象关于点（-1，1）对称；④已知命题：对任意的，都有，则：存在，使得。其中所有真命题的序号是     。

若不等式(a－2)x²+2(a－2)x－4<0对一切x∈R恒成立，则a的取值范围是(    )

A．(－∞,2         B.－2,2     C.(－2,2      D.(－∞,－2)

如图，在△ABC中，设=， =， =, =λ,(0<λ<1), =μ (0<μ<1),试用向量，表示.

已知集合A={z||z－2|≤2,z∈C},集合B={w|w=zi+b,b∈R},当A∩B=B时，求b的值.

（本题20分，第1小题满分4分，第2小题满分6分，第3小题6分，第4小题4分）

         我们知道，判断直线与圆的位置关系可以用圆心到直线的距离进行判别，那么直线与椭圆的位置关系有类似的判别方法吗？请同学们进行研究并完成下面问题。

   （1）设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线的距离分别为d₁、d₂，试求d₁·d₂的值，并判断直线L与椭圆M的位置关系。

   （2）设F₁、F₂是椭圆的两个焦点，点F₁、F₂到直线        （m、n不同时为0）的距离分别为d₁、d₂，且直线L与椭圆M相切，试求d₁·d₂的值。

   （3）试写出一个能判断直线与椭圆的位置关系的充要条件，并证明。

   （4）将（3）中得出的结论类比到其它曲线，请同学们给出自己研究的有关结论（不必证明）。

  若，且恒成立，则的最小值是（     ）

   A.      B.       C.       D. 

（本题满分12分）设函数f (x) = (b，c∈N^*)，若方程f(x) = x的解为0，2，且f (–2)＜–．（Ⅰ）试求函数f(x)的单调区间；（Ⅱ）已知各项不为零的数列{a_n}满足4S_n·f () = 1，其中S_n为{a_n}的前n项和．求证：．

（本小题满分16分）函数其中为常数，且函数和的图像在其与坐标轴的交点处的切线互相平行

（1）、求函数的解析式

（2）、若关于的不等式恒成立，求实数的取值范围。

已知A（—2,4）、B（3,—1）、C（—3,—4）且,,求点M、N的坐标及向量的坐标.

（本小题满分12分

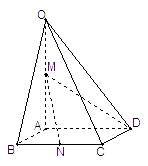如图，在四棱锥中，底面四边长为1的菱形，, , ,为的中点，为的中点

（Ⅰ）证明：直线；

（Ⅱ）求异面直线AB与MD所成角的大小；

（Ⅲ）求点B到平面OCD的距离。