
科目: 来源: 题型:
双曲线x2-ay2=1的焦点坐标是 ( )
A.(![]() , 0) , (-
, 0) , (-![]() , 0) B.(
, 0) B.(![]() , 0), (-
, 0), (-![]() , 0)
, 0)
C.(-![]() , 0),(
, 0),(![]() , 0) D.(-
, 0) D.(-![]() , 0), (
, 0), (![]() , 0)
, 0)
查看答案和解析>>
科目: 来源: 题型:
设F1、F2分别为椭圆C:![]() =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,![]() )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点P是(1)中所得椭圆上的动点,当P在何位置时,![]() 最大,说明理由,并求出最大值。
最大,说明理由,并求出最大值。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某初级中学有三个年级,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 370 | z | 200 |
| 男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目: 来源: 题型:
如图,已知正方体ABCD-A1B1C1D1,AD1与A1D相交于点 O.
(1)判断AD1与平面A1B1CD的位置关系,并证明;
(2)求直线AB1与平面A1B1CD所成的角.
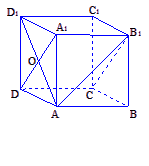
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)已知函数![]() ,且函数
,且函数![]() 的图象关于原点对称,其图象在
的图象关于原点对称,其图象在![]() 处的切线方程为
处的切线方程为![]() (1)求
(1)求![]() 的解析式; (2)是否存在区间
的解析式; (2)是否存在区间![]() 使得函数
使得函数![]() 的定义域和值域均为
的定义域和值域均为![]() ,且其解析式为f(x)的解析式?若存在,求出这样的一个区间[m,n];若不存在,则说明理由.
,且其解析式为f(x)的解析式?若存在,求出这样的一个区间[m,n];若不存在,则说明理由.
查看答案和解析>>
科目: 来源: 题型:
如图,⊙![]() 的直径
的直径![]() 的延长线与弦
的延长线与弦![]() 的延长线相交于点
的延长线相交于点![]() ,
,
![]() 为⊙
为⊙![]() 上一点,AE=AC ,
上一点,AE=AC ,![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,
(1)求![]() 的长度.
的长度.
(2)若圆F且与圆![]() 内切,直线PT与圆F切于点T,求线段PT的长度
内切,直线PT与圆F切于点T,求线段PT的长度

查看答案和解析>>
科目: 来源: 题型:
用数学归纳法证明![]() ,则当n=k+1时左端应在n=k的基础上加上 ( )
,则当n=k+1时左端应在n=k的基础上加上 ( )
A.k2+1 B.(k+1)2
C.![]() D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2.
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com