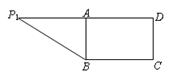
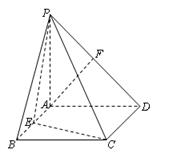
在直角梯形P₁DCB中，P₁D//CB，CD//P₁D且P₁D = 6，BC = 3，DC =，A是P₁D的中点，沿AB把平面P₁AB折起到平面PAB的位置，使二面角P－CD－B成45°角，设E、F分别是线段AB、PD的中点．

   （1）求证：AF//平面PEC；

   （2）求平面PEC和平面PAD所成的二面角的大小；

   （3）求点D到平面PEC的距离．

已知是一个棱长为1的正方体，是底面的中心，是棱上的点，且，则的面积为　　　

求经过A（2，），和直线相切，且圆心在直线上的圆的方程

已知函数f(x)=x³+ax²+bx+c，过曲线y=f(x)上的点P(1，f(1))的切线方程为y=3x+1．

       (Ⅰ)若函数f(x)在x=－2处有极值，求f(x)的表达式；

       (Ⅱ)若函数y=f(x)在区间[－2,1]上单调递增，求实数b的取值范围．

（本题满分12分）已知函数（x>0）．（1）若b≥，求证≥（e是自然对数的底数）；（2）设F(x)=+（x≥1，a∈R），试问函数F(x)是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

某城市有甲、乙、丙、丁4个旅游景点，一位客人游览这4个景点的概率都是0.6，且客人是否游览哪个景点互不影响．设表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．

（1）求的分布列及数学期望；

（2）记“函数在区间上单调递增”为事件A，求事件A的概率．

直角坐标系中，O为坐标原点，设直线经过点，且与轴交于

点F（2，0）。

   （I）求直线的方程；

   （II）如果一个椭圆经过点P，且以点F为它的一个焦点，求椭圆的标准方程。

从10个元件中（其中4个相同的甲品牌元件和6个相同的乙品牌元件）随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为，每个乙品牌元件能通过测试的概率均为.试求：

（I）选出的3个元件中，至少有一个甲品牌元件的概率；

（II）若选出的三个元件均为乙品牌元件，现对它们进行性能测试，求至少有两个乙品牌元件同时通过测试的概率.

如图，四边形ABCD是一个边长为100米的正方形地皮，其中ATPS是一半径为90米的扇形小山，其余部分都是平地，P是弧TS上一点，现有一位开发商想在平 地上建造一个两边落在BC与CD上的长方形停车场PQCR.

（Ⅰ）若∠PAT=θ，试写出四边形RPQC的面积S关于θ

          的函数表达式，并写出定义域；

      （Ⅱ）试求停车场的面积最大值。

已知向量a=(2cosα,2sinα),b=(3cosβ,3sinβ),若a与b的夹角为60°,则直线xcosα-ysinα+=0与圆(x-cosβ)²+(y+sinβ)²=1的位置关系是(    )

A.相交             B.相交且过圆心      C.相切               D.相离