如图，三棱锥中，底面于，，点分别是的中点，求二面角的余弦值．

袋中装有大小相同的白球、红球和黄球，白球和红球共有5个，现从中任取2个球，每取得一个白球得1分，每取得一个红球得2分，每取得一个黄球得0分，用表示所得分数，已知得0分的概率为，得1分的概率为

（1）袋中白球，红球，黄球的个数；

（2）的概率分布列及数学期望E.

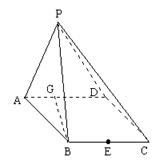
如图，在四棱锥P—ABCD中，底面ABCD是∠DAB=60°且边长为1的菱形。侧面PAD是正三角形，其所在侧面垂直底面ABCD，G是AD中点。

（1）求异面直线BG与PC所成的角；

（2）求点G到面PBC的距离；

（3）若E是BC边上的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并说明理由。

求长短轴之比为3∶2，一个焦点是(0,-2)，中心在原点的椭圆的标准方程

某租凭公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出，当每辆车的月租金每增加50元时，未租出的车将会增加一辆，租出的车每辆每月需要维护费200元。

   （1）当每辆车的月租金定为3600元时，能租出多少辆车？

   （2）当每辆车的月租金为多少元时，租凭公司有月收益最大？最大月收益是多少元？

（本题满分14分）

设数列{a_n}的各项均为正数，它的前n项和为S_n（n∈N*），已知点(a_n，4S_n)在函数f (x)=x²+2x+1的图象上．（1）证明{a_n}是等差数列，并求a_n；（2）设m、k、p∈N*，m+p=2k，求证：＋≥；（3）对于（2）中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由。

在平面直角坐标系中，已知圆心在直线上，半径为的圆C经过坐标原点O，椭圆与圆C的一个交点到椭圆两焦点的距离之和为10.

（1）求圆C的方程；

（2）若F为椭圆的右焦点，点P在圆C上，且满足，求点P

某小区要建一座八边形的休闲小区，它的主体造型的平面图是由二个相同的矩形ABCD和EFGH构成的面积为200 m²的十字型地域，计划在正方形MNPQ上建一座“观景花坛”，造价为4200元／m²，在四个相同的矩形上(图中阴影部分)铺花岗岩地坪，造价为210元/m²,再在四个空角（如ΔDQH等）上铺草坪，造价为80元/m²。

设总造价为S元，AD长为xm,试建立S与x的函数关系；

当x为何值时，S最小？并求这个最小值。

某同学上楼梯的习惯每步走1阶或2阶，现有一个11阶的楼梯 ，该同学从第1阶到第11阶用7步走完。

(1)求该同学恰好有连着三步都走2阶的概率；

(2)记该同学连走2阶的最多步数为ζ，求随机事件ζ的分布列及其期望。

（本题12分）已知命题p：|4-x|≤6，q：x²-2x+1- a²≥0（a>0），若非p是q的充分不必要条件，求a的取值范围。