（安徽卷理20）设函数

（Ⅰ）求函数的单调区间；

（Ⅱ）已知对任意成立，求实数的取值范围。

（安徽卷文20）设函数为实数。

（Ⅰ）已知函数在处取得极值，求的值；

（Ⅱ）已知不等式对任意都成立，求实数的取值范围。

（北京卷理18）已知函数，求导函数，并确定的单调区间．

（北京卷文17）已知函数，且是奇函数．

（Ⅰ）求，的值；

（Ⅱ）求函数的单调区间．

（福建卷理22）已知函数f(x)=ln(1+x)-x₁

（Ⅰ）求f(x)的单调区间；

（Ⅱ）记f(x)在区间（n∈N*）上的最小值为b_x令a_n=ln(1+n)-b_x.

（Ⅲ）如果对一切n，不等式恒成立，求实数c的取值范围；

（Ⅳ）求证：  

（福建卷文21）已知函数的图象过点（-1，-6），且函数的图象关于y轴对称.

(Ⅰ)求m、n的值及函数y=f(x)的单调区间；

(Ⅱ)若a＞0，求函数y=f(x)在区间（a-1,a+1）内的极值.

（广东卷文17）某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算，如果将楼房建为x(x≥10)层，则每平方米的平均建筑费用为560+48x（单位：元）.为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？

（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝）

（海南宁夏卷理21）设函数，曲线在点处的切线方程为。

（1）求的解析式；

（2）证明：曲线的图像是一个中心对称图形，并求其对称中心；

（3）证明：曲线上任一点处的切线与直线和直线所围三角形的面积为定值，并求出此定值。

（海南宁夏卷文21）设函数，曲线在点处的切线方程为

。

（1）求的解析式；

（2）证明：曲线上任一点处的切线与直线和直线所围成的三角形面积为定值，并求此定值。

（湖北卷理20）水库的蓄水量随时间而变化，现用表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于的近似函数关系式为

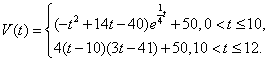
（Ⅰ）该水库的蓄求量小于50的时期称为枯水期.以表示第1月份（）,同一年内哪几个月份是枯水期？

（Ⅱ）求一年内该水库的最大蓄水量（取计算）.