
科目: 来源: 题型:
已知无穷数列{an},Sn是其前n项和,对不小于2的正整数n,满足关系![]() .
.
(1)求a1,a2,a3;(2)用数学归纳法证明求数列{an}的通项公式.
(3)设![]() 计算
计算![]()
查看答案和解析>>
科目: 来源: 题型:
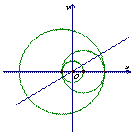 设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
设M1(0,0),M2(1,0),以M1为圆心,| M1 M2 | 为半径作圆交x轴于点M3 (不同于M2),记作⊙M1;以M2为圆心,| M2 M3 | 为半径作圆交x轴于点M4 (不同于M3),记作⊙M2;……;以Mn为圆心,| Mn Mn+1 | 为半径作圆交x轴于点Mn+2 (不同于Mn+1),记作⊙Mn;……当n∈N*时,过原点作倾斜角为30°的直线与⊙Mn交于An,Bn.考察下列论断:
当n=1时,![]() ;Ks当n=2时,
;Ks当n=2时,![]() ;当n=3时,
;当n=3时,![]() ;
;
当n=4时, ![]() ;当n=5时,
;当n=5时, ![]() ;……,
;……,
则推测一个一般的结论:对于n∈N*,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分10分)
已知构成某系统的元件能正常工作的概率为p(0<p<1),且各个元件能否正常工作是相互独立的.今有2n(n大于1)个元件可按下图所示的两种联结方式分别构成两个系统甲、乙.
(1)试分别求出系统甲、乙能正常工作的概率p1,p2;
(2)比较p1与p2的大小,并从概率意义上评价两系统的优劣.
 |  | ||
查看答案和解析>>
科目: 来源: 题型:
(本小题满分14分)已知各项均不为零的数列{an}的前n项和为Sn,且满足a1=c,
2Sn=an an+1+r.
(1)若r=-6,数列{an}能否成为等差数列?若能,求![]() 满足的条件;若不能,请说明理由;
满足的条件;若不能,请说明理由;
(2)设![]() ,
,![]() ,
,
若r>c>4,求证:对于一切n∈N*,不等式![]() 恒成立.
恒成立.
查看答案和解析>>
科目: 来源: 题型:阅读理解
(本大题18分)
阅读下面所给材料:已知数列{an},a1=2,an=3an–1+2,求数列的通项an。
解:令an=an–1=x,则有x=3x+2,所以x= –1,故原递推式an=3an–1+2可转化为:
an+1=3(an–1+1),因此数列{an+1}是首项为a1+1,公比为3的等比数列。
根据上述材料所给出提示,解答下列问题:
已知数列{an},a1=1,an=3an–1+4,
(1)求数列的通项an;并用解析几何中的有关思想方法来解释其原理;
(2)若记Sn=![]() ,求
,求![]() Sn;
Sn;
(3)若数列{bn}满足:b1=10,bn+1=100![]() ,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
,利用所学过的知识,把问题转化为可以用阅读材料的提示,求出解数列{bn}的通项公式bn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com