
科目: 来源: 题型:
(本题满分12分)
在“环境保护低碳生活知识竞赛”第一环节测试中,设有A、B、C三道必答题,分值依次为20分、30分、50分.竞赛规定:若参赛选手连续两道题答题错误,则必答题总分记为零分;否则各题得分之和记为必答题总分已知某选手回答A、B、C三道题正确的概率分别为![]() 、
、![]() 、
、![]() ,且回答各题时相互之间没有影响
,且回答各题时相互之间没有影响
(I) 若此选手按A、B、C的顺序答题,求其必答题总分为70分的概率;
(Ⅱ).若此选手可以自由选择答题顺序,求其必答题总分为50分的概率;
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分) “石头、剪刀、布”是一种广泛流传于我国民间的古老游戏,其规则是:用三种不同的手势分别表示石头、剪刀、布;两个玩家同时出示各自手势1次记为1次游戏, “石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”;双方出示的手势相同时,不分胜负.现假设玩家甲、乙双方在游戏时出示三种手势是等可能的.
(Ⅰ)写出玩家甲、乙双方在1次游戏中出示手势的所有可能结果;
(Ⅱ)求出在1次游戏中玩家甲不输于玩家乙的概率.
查看答案和解析>>
科目: 来源: 题型:
一袋中有红、黄、蓝三种颜色的小球各一个,每次从中取出一个,记下颜色后放回,当三种颜色的球全部取出时停止取球,则恰好取5次球时停止取球的概率为( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等
品通过检测的概率为![]() .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为![]() ,求
,求![]() 的分布列;(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
的分布列;(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
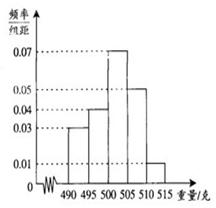
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本,称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() ,…,
,…,![]() ,由此得到样本的频率分布直方图,如右图所示.
,由此得到样本的频率分布直方图,如右图所示.
(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量.
(Ⅱ)在上述抽取的40件产品中任取2件,设![]() 为重量超过505克的产品数量,求
为重量超过505克的产品数量,求![]() 的分布列.
的分布列.
(Ⅲ)从流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.
查看答案和解析>>
科目: 来源: 题型:
(本题满分12分)
 某校从参加高一年级期中考试的学生中随机抽出
某校从参加高一年级期中考试的学生中随机抽出![]() 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在![]() 内的频率,并补全这个
内的频率,并补全这个
频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组
区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从![]() 名学生中随机抽取
名学生中随机抽取![]() 人,抽到
人,抽到
的学生成绩在![]() 记
记![]() 分,在
分,在![]() 记
记![]() 分,
分,
在![]() 记
记![]() 分,用
分,用![]() 表示抽取结束后的总记分,
表示抽取结束后的总记分,
求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
某工厂生产甲、乙两种产品,每种产品都是经过第一道和第二道工序加工而成,两道工序的加工结果相互独立,每道工序的加工结果均有![]() 、
、![]() 两个等级,对每种产品,两道工序的加工结果都为
两个等级,对每种产品,两道工序的加工结果都为![]() 级时,产品为一等品,其余均为二等品
级时,产品为一等品,其余均为二等品
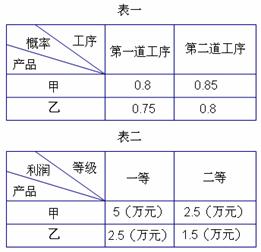
(1)已知甲、乙两种产品每一道工序的加工结果为![]() 级的概率如表一所示,分别求生产的甲、乙产品为一等品的概率
级的概率如表一所示,分别求生产的甲、乙产品为一等品的概率![]() 、
、![]() ;
;
(2)已知一件产品的利润如表二所示,用![]() 、
、![]() 分别表示一件甲、乙产品的利润,在(1)的条件下,分别求甲、乙两种产品利润的分布列及数学期望。
分别表示一件甲、乙产品的利润,在(1)的条件下,分别求甲、乙两种产品利润的分布列及数学期望。
查看答案和解析>>
科目: 来源: 题型:
(本小题满分12分)
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0.88,用![]() 表示该学生选修的课程门数和没有选修的课程门数的乘积.
表示该学生选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)记“函数![]() 为R上的偶函数”为事件A,求事件A的概率;
为R上的偶函数”为事件A,求事件A的概率;
(Ⅱ)求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com