如图，质点在半径为2的圆周上逆时针运动，其初始位置为（，），角速度为1，那么点到轴距离关于时间的函数图像大致为

如果若干个函数的图象经过平移后能够重合，则这些函数为“互为生成”函数，给出下列函数，其中与构成“互为生成”函数的为         

A．                   B.

C．        D.

已知f (x) = sin (x +)，g (x) = cos (x－)，则下列命题中正确的是

A．函数y = f (x) · g (x) 的最小正周期为2p

B．函数y = f (x) · g (x) 是偶函数

C．函数y = f (x) + g (x) 的最小值为－1

D．函数y = f (x) + g (x) 的一个单调增区间是

用平方米的材料制成一个有盖的圆锥形容器，如果在制作过程中材料无损耗，且材料的厚度忽略不计，底面半径长为，圆锥母线的长为

（1）、建立与的函数关系式，并写出的取值范围；（6分）

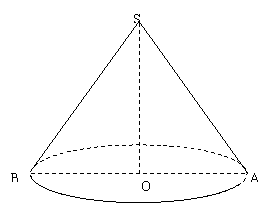（2）、圆锥的母线与底面所成的角大小为，求所制作的圆锥形容器容积多少立方米(精确到0. 01m³) （6分）

（本小题满分16分）

如图，实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成，圆P和圆Q的

半径都是2km，点P在圆Q上，现要在公园内建一块顶点都在圆P上的多边形活动场地．

（1）如图甲，要建的活动场地为△RST，求场地的最大面积；

（2）如图乙，要建的活动场地为等腰梯形ABCD，求场地的最大面积．

（本小题满分14分）春节期间，某地昼夜气温呈周期性变化，温度随时间变化近似满足函数（，，）（如图4），且在每天凌晨时达到最低温度℃，在下午时达到最高温度℃．

⑴求这段时间气温随时间变化的函数解析式；

⑵这段时间该地一昼夜内哪几个时刻的气温为℃？

注：一昼夜指从凌晨0时（含）到午夜24时（不含）．

如图，线段=8，点在线段上，且=2，为线段上一动点，点绕点旋转后与点绕点旋转后重合于点.设=， 的面积为.则的定义域为        ； 的零点是         . 

设偶函数（的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL＝1，则的值为

 (A)            (B)  

 (C)              (D)

(本小题满分14分)

如图所示，某市准备在一个湖泊的一侧修建一条直路；另一侧修建一条观光大道,它的前一段是以为顶点,轴为对称轴,开口向右的抛物线的一部分,后一段是函数时的图象,图象的最高点为,

,垂足为．

(Ⅰ)求函数的解析式.

(Ⅱ)若在湖泊内修建如图所示的矩形水上乐园,

问点落在曲线上何处时,水上乐园的面积最大？

（本小题满分12分）

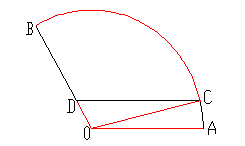
如图扇形AOB是一个观光区的平面示意图，其中∠AOB的圆心角为，半径OA为1Km，为了便于游客观光休闲，拟在观光区内铺设一条从入口A到出口B的观光道路，道路由圆弧AC、线段CD及线段BD组成。其中D在线段OB上，且CD//AO，设∠AOC=θ，

用θ表示CD的长度，并写出θ的取值范围。

当θ为何值时，观光道路最长？