
科目: 来源: 题型:
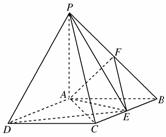
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(1)求三棱锥E-PAD的体积;
(2)点![]() E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在BC边的何处,都有PE⊥AF.
查看答案和解析>>
科目: 来源: 题型:
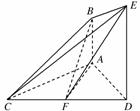
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)若∠CAD=90°,求三棱锥F-BCE的体积.
查看答案和解析>>
科目: 来源: 题型:
如图,四棱锥P-A![]() BCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
BCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(1)求证:平面AEC⊥平面PDB;
 (2)若E为PB的中点,棱PC(不包括端点)
(2)若E为PB的中点,棱PC(不包括端点)![]() 上是否存在点F,使得DF∥平面AEC,若存在,找出点F的位置,若不存在,说明理由.
上是否存在点F,使得DF∥平面AEC,若存在,找出点F的位置,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
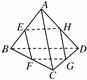
如![]() 图,ABCD是空间四边形,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,
图,ABCD是空间四边形,E、F、G、H分别是四边上的点,它们共面,并且AC∥平面EFGH,![]() BD∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,AE∶EB=______.
BD∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,AE∶EB=______.
查看答案和解析>>
科目: 来源: 题型:
如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足________时,有MN∥平面B1BDD1.![]()
查看答案和解析>>
科目: 来源: 题型:
设m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分而不必要条件是( )
A.m∥β且l1∥α B.m∥l1且n∥l2
C.m∥β且n∥β D.m∥β且n∥l2
查看答案和解析>>
科目: 来源: 题型:
已知平面α∥平面β,P是α、β外一点,过点P的直线m与α、β分别交于A、C,过点P的直线n与α、β分别交于B、D且PA=6,AC=9,PD=8,则BD的长为( )
A.16 B.24或![]()
C.14 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com