对于函数，若存在∈R，使成立，则称为的不动点．如果函数＝有且仅有两个不动点0和2．

（1）试求b、c满足的关系式；

（2）若c＝2时，各项不为零的数列{a_n}满足4S_n·＝1，

求证：＜＜；

   （3）在(2)的条件下, 设b_n＝－，为数列{b_n}的前n项和，

        求证：．

已知函数的导函数是, 对任意两个不相等

的正数, 证明: (1)当时, ;

                     (2)当时, .

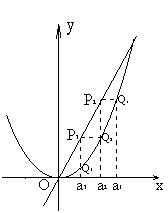
如图,已知直线及曲线上的点的横坐标为().从曲线上的点作直线平行于轴，交直线作直线平行于轴，交曲线的横坐标构成数列.

(1)试求的关系;

(2)若曲线的平行于直线的切线的切点恰好介于点之间(不与重合),求的取值范围;

(3)若,求数列的通项公式.

已知函数的图像在点处的切线方程为.

（1）用表示出；

（2）若在上恒成立，求的取值范围；

（3）证明：.

设，函数， ，．

（1）当时，求函数的值域；

（2）试讨论函数的单调性．

数列满足，且时，，

（1）       求数列的通项公式；

（2）       设数列的前项和为，求证对任意的正整数都有

已知数列的前项和的平均数为

（1）求的通项公式；

（2）设，试判断并说明的符号；

（3）设函数，是否存在最大的实数? 当时，对于一切非零自然数，都有

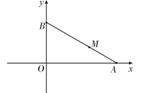
 如图，长为m＋1（m＞0）的线段AB的两个端点A和B分别在x轴和y轴上滑动，点M是线段AB上一点，且．

（1）求点M的轨迹Γ的方程，并判断轨迹Γ为何种圆锥曲线；

（2）设过点Q(，0)且斜率不为0的直线交轨迹Γ于C、D两点．

试问在x轴上是否存在定点P，使PQ平分∠CPD？若存在，求点P的坐标；

若不存在，请说明理由．

已知抛物线与双曲线有公共焦点，点

   是曲线在第一象限的交点，且．

（1）求双曲线的方程；

（2）以双曲线的另一焦点为圆心的圆与直线相切，圆：

    ．过点作互相垂直且分别与圆、圆相交的直线和，设被圆截得的弦长为，被圆截得的弦长为．是否为定值？请说明理由．

．某地区有荒山2200亩，从2002年开始每年年初在荒山上植树造林，

第一年植树100亩，以后每年比上一年多植树50亩．

（1）若所植树全部成活，则到哪一年可以将荒山全部绿化？

（2）若每亩所植树苗木材量为2立方米，每年树木木材量的自然增长率为20％，那么到全部绿化后的那一年年底，该山木材总量是多少？（精确到１立方米, ）