如图，在复平面内，点表示复数，则图中表示的共轭复数的点是（    ）

（A）           （B）  （C）        （D）

设集合，集合，则（    ）

（A）                                 （B）

（C）                               （D）

不等式选讲

设a，b，c均为正数，且a+b+c=1，证明：

（Ⅰ）

（Ⅱ）

坐标系与参数方程

已知动点P，Q都在曲线C： 上，对应参数分别为β=α

                               与α=2π为（0＜α＜2π）M为PQ的中点。

（Ⅰ）求M的轨迹的参数方程

（Ⅱ）将M到坐标原点的距离d表示为a的函数，并判断M的轨迹是否过坐标原点。

选修4-1几何证明选讲                  

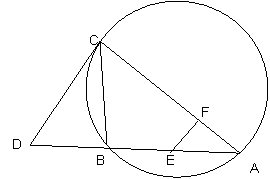
如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E、F分别为弦AB与弦AC上的点，且BC•AE=DC•AF，B、E、F、C四点共圆。

（1）       证明：CA是△ABC外接圆的直径；

（2）       若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值。                       

已知函数f(x)=e^x-ln(x+m)

(Ι)设x=0是f(x)的极值点，求m,并讨论f(x)的单调性；

（Ⅱ）当m≤2时，证明f(x)>0

平面直角坐标系xOy中，过椭圆M：(a>b>0)右焦点的直线x+y-=0交M于A，B两点，P为AB的中点，且OP的斜率为

(Ι)求M的方程

（Ⅱ）C,D为M上的两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值

    经销商经销某种农产品，在一个销售季度内，每售出1t该产品获利润500元，未售出的产品，每1t亏损300元。根据历史资料，得到销售季度内市场需求量的频率分布直方图，如右图所示。经销商为下一个销售季度购进了130t该农产品。以x（单位：t，

100≤x≤150）表示下一个销售季度内经销该农产品的利润。

    （Ⅰ）将T表示为x的函数

    （Ⅱ）根据直方图估计利润T，不少于57000元的概率；

（Ⅲ）在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，

需求量落入该区间的频率作为需求量取该区间中点值的概率（例如：若x）则取x=105，且x=105的概率等于需求量落入的利润T的数学期望。

如图，直棱柱ABC-A1B1C1中，D，E分别是AB，BB1的中点，

AA1=AC=CB=AB。

（Ⅰ）证明：BC1//平面A1CD

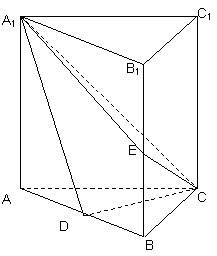（Ⅱ）求二面角D-A1C-E的正弦值

△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB。

（Ⅰ）求B；

（Ⅱ）若b=2，求△ABC面积的最大值。