
科目: 来源: 题型:
已知椭圆C的中心在的点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线![]() 与椭圆交于A,B两点,
与椭圆交于A,B两点,![]() 的面积为4,
的面积为4,![]() 的周长为
的周长为![]()
(I)求椭圆C的方程;
(II)设点Q的从标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
如图所示,已知![]() 中,
中,![]() AB=2OB=4,若
AB=2OB=4,若![]() 是
是![]() 绕直线AO旋转而成的,记二面角B—AO—C的大小为
绕直线AO旋转而成的,记二面角B—AO—C的大小为![]()
(I)若![]() ,求证:平面
,求证:平面![]() 平面AOB;
平面AOB;
(II)若![]() 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。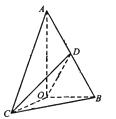
查看答案和解析>>
科目: 来源: 题型:
2010年广东亚运会,某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作,比赛时每位运动员自选一个系列完成,两个动作得分之和为该运动员的成绩。假设每个运动员完成每个系列中的两个动作的得分是相互独立的,根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
甲系列:
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |
|
|
|
|
乙系列:
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |
|
|
|
|
现该运动员最后一个出场,其之前运动员的最高得分为118分。
(I)若该运动员希望获得该项目的第一名,应选择哪个系列,说明理由,并求其获得第一名的
概率;
(II)若该运动员选择乙系列,求其成绩X的分布列及其数学期望EX。
查看答案和解析>>
科目: 来源: 题型:
对于函数![]() 与函数
与函数![]() 有下
有下
列命题:
①函数![]() 的图像关于
的图像关于![]() 对称;
对称;
②函数![]() 有且只有一个零点;
有且只有一个零点;
③函数![]() 和函数
和函数![]() 图像上存在平行的切线;
图像上存在平行的切线;
④若函数![]() 在点P处的切线平行于函数
在点P处的切线平行于函数![]() 在点Q处的切线,则直线PQ的斜率为
在点Q处的切线,则直线PQ的斜率为![]()
其中正确的命题是 。(将所有正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com