
科目: 来源:2010-2011年辽宁省开原高中高二下学期第二次考试理数 题型:解答题
(12分)在某社区举办的“2010亚运知识有奖问答比赛”中,甲、乙、丙三人同时回答一道有关亚运知识的问题,已知甲回答这道题对的概率为 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 ;
;
(1)求乙、丙两人各自回答这道题对的概率;
(2)用 表示回答该题对的人数,求
表示回答该题对的人数,求 的分布列和
的分布列和 .
.
查看答案和解析>>
科目: 来源:2010-2011学年安徽省亳州市涡阳二中高二第二学期期末质量检测理科数学试题 题型:解答题
射击比赛中,每位射手射击队10次,每次一发,击中目标得3分,未击中目标得0分,每射击一次,凡参赛者加2分,已知小李击中目标的概率为0.8.
(1)设X为小李击中目标的次数,求X的概率分布;
(2)求小李在比赛中的得分的数学期望与方差
查看答案和解析>>
科目: 来源:2010—2011学年河南郑州市第47中学高二下学期第二次月考试题数学(理科) 题型:解答题
将一个半径适当的小球放入如图所示的容器最上方的入口处, 小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是 .
.
(Ⅰ)求小球落入A袋中的概率P(A);
(Ⅱ)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX.
查看答案和解析>>
科目: 来源:2011年陕西省普通高等学校招生统一考试理科数学 题型:解答题
本小题满分13分)
如图,A地到火车站共有两条路径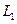 和
和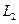 ,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 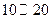 | 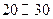 | 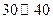 |  | 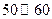 |
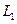 的频率 的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
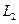 的频率 的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
查看答案和解析>>
科目: 来源:2010-2011学年广东惠阳高级中学高二第二学期第二次段考数学试题(理科) 题型:解答题
某重点高校数学教育专业的三位毕业生甲,乙,丙参加了一所中学的招聘面试,面试合格者可以正式签约,毕业生甲表示只要面试合格就签约,毕业生乙和丙则约定:两人面试合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合格互不影响,求:(1)至少有1人面试合格的概率;(2)签约人数X的分布列及数学期望。
,且面试是否合格互不影响,求:(1)至少有1人面试合格的概率;(2)签约人数X的分布列及数学期望。
查看答案和解析>>
科目: 来源:2011年湖南省普通高等学校招生统一考试文科数学 题型:解答题
(本题满分12分)
某河流上的一座水力发电站,每年六月份的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关.据统计,当X=70时,Y=460;X每增加10,Y增 加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(I)完成如下的频率分布表:
近20年六月份降雨量频率分布表
| 降雨量 | 70 |  110 110 | 140 | 160 | 200 | 220 |
| 频率 |  | |  | | |  |
 年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.查看答案和解析>>
科目: 来源:2011年江西省普通高中招生考试理科数学 题型:解答题
四.本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令X表示此人选对A饮料的杯数.假设次人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
查看答案和解析>>
科目: 来源:2011年江西省普通高中招生考试文科数学 题型:解答题
(本小题满分12分)
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5
杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工
一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3
杯选对2杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
查看答案和解析>>
科目: 来源:2011届广东省深圳高级中学高三高考最后模拟考试理数 题型:解答题
(本小题满分12分)甲有一个装有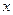 个红球、
个红球、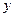 个黑球的箱子,乙有一个装有
个黑球的箱子,乙有一个装有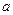 个红球、
个红球、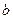 个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(
个黑球的箱子,两人各自从自己的箱子里任取一球,并约定:所取两球同色时甲胜,异色时乙胜(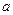 ,
,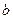 ,
,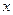 ,
,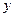
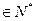 ).
).
(Ⅰ)当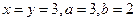 ,时,求甲获胜的概率;
,时,求甲获胜的概率;
(Ⅱ)当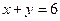 ,
,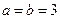 时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的
时,规定:甲取红球获胜得3分;取黑球获胜得1分;甲负得0分.求甲的得分期望达到最大时的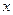 ,
,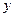 值;
值;
(Ⅲ)当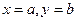 时,这个游戏规则公平吗?请说明理由.
时,这个游戏规则公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com