
科目: 来源:2010-2011年北京市通州区高二下学期期末考试理科数学 题型:解答题
(本题6分)某学校组织课外活动小组,其中三个小组的人员分布如下表(每名同学只参加一个小组):
| | 棋类小组 | 书法小组 | 摄影小组 |
| 高中 | a | 6 | 12 |
| 初中 | 7 | 4 | 18 |
 效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。
效果进行抽样调查,按分层抽样的方法从小组成员中抽取6人,结果摄影小组被抽出3人。查看答案和解析>>
科目: 来源:2010-2011年北京市东城区高一下学期期末考试数学 题型:解答题
(本题9分)甲袋中有3只白球、7只红球、1 5只黑球;乙袋中有10只白球、6只红球、9只黑球。
5只黑球;乙袋中有10只白球、6只红球、9只黑球。
(1)从甲袋中任取一球,求取到白球的概率;
(2)从两袋中各取一球,求两球颜色相同的概率;
(3)从两袋中各取一球,求两球颜色不同的概率。
查看答案和解析>>
科目: 来源:2011-2012年辽宁省庄河六高高二上学期开学初考试联考理科数学 题型:解答题
做投掷2颗骰子试验,用( x,y)表示点P的坐标,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数.
x,y)表示点P的坐标,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数.
(1)求点P在直线y=x上的概率
( 2)求点P不在直线y=x+1上的概率
2)求点P不在直线y=x+1上的概率
(3)求 点P的坐标(x,y)满足16<
点P的坐标(x,y)满足16< 的概率
的概率
查看答案和解析>>
科目: 来源:2010-2011年云南省玉溪一中高二下学期期末考试理数 题型:解答题
(本小题满分10分)
某地区为下岗女职工免费提供财会和家政培训,以提高下岗女职工的再就业能力,每名下岗人员可以参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有50%,参加过家政培训的有80%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响
(1)任选1名下岗女职工,求该人参加过培训的概率
(2)任选3名下岗女职工,记 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求 的分布列和期望
的分布列和期望
查看答案和解析>>
科目: 来源:2011届贵州省五校高三第五次联考文科数学(暨遵义四中第13次月考) 题型:解答题
甲盒有标号分别为1、2、3的3个红球;乙盒有标号分别为1、2、…、

的 个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和
个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和 号黑球的概率为
号黑球的概率为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)现从甲乙两盒各随机抽取1个小球,抽得红球的得分为其标号数;抽得黑球,若标号数为奇数,则得分为1,若标号数为偶数,则得分为0.求得分为2的概率.
查看答案和解析>>
科目: 来源:2010-2011学年贵州省遵义四中高二下学期期末考试文科数学 题型:解答题
(本小题满分12分) 甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是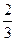 ,乙取胜的概率为
,乙取胜的概率为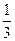 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
查看答案和解析>>
科目: 来源:2010-2011学年贵州省遵义四中高二下学期期末考试文科数学 题型:解答题
(本小题满分12分)学习小组有6个同学,其中4个同学从来没有参加过数学研究性学习活动,2个同学曾经参加过数学研究性学习活动.
(1)现从该小组中任选2个同学参加数学研究性学习活动,求恰好选到1个曾经参加过数学研究性学习活动的同学的概率;
(2)若从该小组中任选2个同学参加数学研究性学习活动,活动结束后,求该小组没有参加过数学研究性学习活动的同学个数 取2,3,4时的概率
取2,3,4时的概率
查看答案和解析>>
科目: 来源:2010-2011学年贵州省遵义四中高二下学期期末考试文科数学 题型:解答题
(本小题满分10分)某种有奖销售的饮料,瓶盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一瓶该饮料。
.甲、乙、丙三位同学每人购买了一瓶该饮料。
(Ⅰ)求三位同学都没有中奖的概率;
(Ⅱ)求三位同学中至少有两位没有中奖的概率.
查看答案和解析>>
科目: 来源:2011届贵州省五校高三第五次联考理科数学(暨遵义四中第13次月考) 题型:解答题
甲盒有标号分别为1、2、3的3个红球;乙盒有标号分别为1、2、…、

的 个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和
个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和 号黑球的概率为
号黑球的概率为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)现从甲乙两盒各随机抽取1个小球,抽得红球的得分为其标号数;抽得黑球,若标号数为奇数,则得分为1,若标号数为偶数,则得分为0,设被抽取的2个小球得分之和为 ,求
,求 的数学期望
的数学期望 .
.
查看答案和解析>>
科目: 来源:2010-2011学年贵州省遵义四中高二下学期期末考试理科数学 题型:解答题
(本小题满分12分) 甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是 ,乙取胜的概率为
,乙取胜的概率为 ,且每局比赛的胜负是独立的,试求下列问题:
,且每局比赛的胜负是独立的,试求下列问题:
(Ⅰ)比赛以甲3胜1而结束的概率;
(Ⅱ)比赛以乙3胜2而结束的概率;
(Ⅲ)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com