已知正实数x，y满足，则x  y 的最小值为

若（m?0）对一切x≥4恒成立，则实数m的取值范围是

在△ABC中，设角A，B，C的对边分别为a，b，c，且．

（1）求角A的大小；

（2）若，，求边c的大小．

如图，在四棱锥P?ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：

（1）PA∥平面MDB；

（2）PD⊥BC．

甲、乙两地相距1000，货车从甲地匀速行驶到乙地，速度不得超过80，已知货车每小时的运输成本（单位：元）由可变成本和固定成本组成，可变成本是速度平方的倍，固定成本为a元．

（1）将全程运输成本y（元）表示为速度v（）的函数，并指出这个函数的定义域；

（2）为了使全程运输成本最小，货车应以多大的速度行驶？

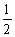如图，已知椭圆的右顶点为A（2，0），点P（2e，）在椭圆上（e为椭圆的离心率）．

（1）求椭圆的方程；

（2）若点B，C（C在第一象限）都在椭圆上，满足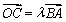，且，求实数λ的值．

设数列{an}满足an1=2ann2?4n1．

（1）若a1?3，求证：存在（a，b，c为常数），使数列{anf(n)}是等比数列，并求出数列{an}的通项公式；

（2）若an是一个等差数列{bn}的前n项和，求首项a1的值与数列{bn}的通项公式．

已知a，b为常数，a?0，函数．

（1）若a=2，b=1，求在（0，∞）内的极值；

（2）①若a>0，b>0，求证：在区间[1，2]上是增函数；

②若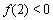，，且在区间[1，2]上是增函数，求由所有点形成的平面区域的面积．

如图，MN为两圆的公共弦，一条直线与两圆及公共弦依次交于A，B，C，D，E，

求证：AB·CD=BC·DE．

已知a，b，若=所对应的变换TM把直线2x?y=3变换成自身，试求实数a，b．