
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:填空题
已知某个几何体的三视图如右图所示,根据图中标出的尺寸,可得这个几何体的表面积是 .

查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:填空题
桌面上有形状大小相同的白球、红球、黄球各3个,相同颜色的球不加以区分,将此9个球排成一排共有 种不同的排法.(用数字作答)
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:填空题
定义: ,其中
,其中 是虚数单位,
是虚数单位, ,且实数指数幂的运算性质对
,且实数指数幂的运算性质对 都适应.若
都适应.若 ,
, ,则
,则 .
.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:填空题
已知函数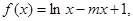 其中
其中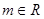 ,
,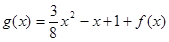 .
.
(1)若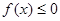 在
在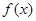 的定义域内恒成立,则实数
的定义域内恒成立,则实数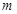 的取值范围
;
的取值范围
;
(2)在(1)的条件下,当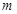 取最小值时,
取最小值时,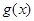 在
在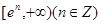 上有零点,则
上有零点,则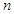 的最大值为
.
的最大值为
.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
已知函数 ,
, .求:
.求:
(1)函数 的最小值及取得最小值的自变量
的最小值及取得最小值的自变量 的集合;
的集合;
(2)函数 的单调增区间.
的单调增区间.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
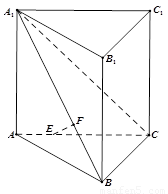
如图,在直三棱柱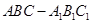 (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面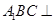 侧面
侧面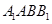 ,
,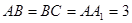 ,
,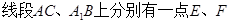 ,且满足
,且满足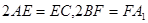 .
.
(1)求证: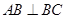 ;
;
(2)求点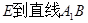 的距离;
的距离;
(3)求二面角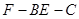 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
长沙市某中学在每年的11月份都会举行“社团文化节”,开幕式当天组织举行大型的文艺表演,同时邀请36名不同社团的社长进行才艺展示.其中有 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生.
(1)若校园电视台记者随机采访3位社长,求恰有1人是高一学生且至少有1人是初中学生的概率;
(2)若校园电视台记者随机采访3位初中学生社长,设初二学生人数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
2013年我国汽车拥有量已超过2亿(目前只有中国和美国超过2亿),为了控制汽车尾气对环境的污染,国家鼓励和补贴购买小排量汽车的消费者,同时在部分地区采取对新车限量上号.某市采取对新车限量上号政策,已知2013年年初汽车拥有量为 (
( =100万辆),第
=100万辆),第 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为 ,该年的增长量
,该年的增长量 和
和 与
与 的乘积成正比,比例系数为
的乘积成正比,比例系数为
 其中
其中 =200万.
=200万.
(1)证明: ;
;
(2)用 表示
表示 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
定义:对于两个双曲线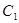 ,
,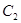 ,若
,若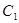 的实轴是
的实轴是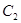 的虚轴,
的虚轴,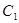 的虚轴是
的虚轴是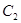 的实轴,则称
的实轴,则称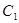 ,
,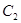 为共轭双曲线.现给出双曲线
为共轭双曲线.现给出双曲线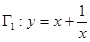 和双曲线
和双曲线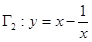 ,其离心率分别为
,其离心率分别为 .
.
(1)写出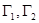 的渐近线方程(不用证明);
的渐近线方程(不用证明);
(2)试判断双曲线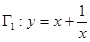 和双曲线
和双曲线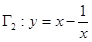 是否为共轭双曲线?请加以证明.
是否为共轭双曲线?请加以证明.
(3)求值: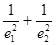 .
.
查看答案和解析>>
科目: 来源:2013-2014学年湖南长沙重点中学高三上学期第四次月考理科数学试卷(解析版) 题型:解答题
设函数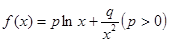 ,若
,若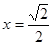 时,
时,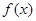 有极小值
有极小值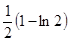 ,
,
(1)求实数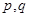 的取值;
的取值;
(2)若数列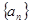 中,
中,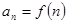 ,求证:数列
,求证:数列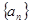 的前
的前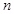 项和
项和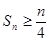 ;
;
(3)设函数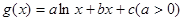 ,若
,若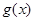 有极值且极值为
有极值且极值为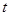 ,则
,则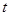 与
与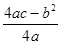 是否具有确定的大小关系?证明你的结论.
是否具有确定的大小关系?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com