
科目: 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
已知各项均为正数的数列{ }满足
}满足 -
- -2
-2 =0,n∈N﹡,且
=0,n∈N﹡,且 是a2,a4的等差中项.
是a2,a4的等差中项.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若 =
=
 ,
, =b1+b2+…+
=b1+b2+…+ ,求
,求 的值.
的值.
查看答案和解析>>
科目: 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
在△ABC中,A、B、C为三个内角,a、b、c为相应的三条边, <C<
<C< ,且
,且 =
= .
.
(1)判断△ABC的形状;
(2)若| +
+ |=2,求
|=2,求 ·
· 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
已知函数f(x)=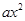 -(a+2)x+lnx.
-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f (1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e)上的最小值为-2,求a的取值范围.
查看答案和解析>>
科目: 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
已知A(-5,0),B(5,0),动点P满足| |,
|, |
| |,8成等差数列.
|,8成等差数列.
(1)求P点的轨迹方程;
(2)对于x轴上的点M,若满足| |·|
|·| |=
|= ,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
,则称点M为点P对应的“比例点”.问:对任意一个确定的点P,它总能对应几个“比例点”?
查看答案和解析>>
科目: 来源:2013-2014学年河南省原名校高三上学期期联考理科数学试卷(解析版) 题型:解答题
设函数f(x)= +
+ ,g(x)=
,g(x)=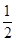 ln(2ex)(其中e为自然对数的底数)
ln(2ex)(其中e为自然对数的底数)
(1)求y=f(x)-g(x)(x>0)的最小值;
(2)是否存在一次函数h(x)=kx+b使得f(x)≥h(x)且h(x)≥g(x)对一切x>0恒成立;若存在,求出一次函数的表达式,若不存在,说明理由:
3)数列{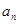 }中,a1=1,
}中,a1=1,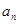 =g(
=g(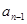 )(n≥2),求证:
)(n≥2),求证: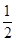 <
<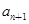 <
<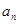 <1且
<1且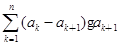 <
<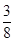 .
.
查看答案和解析>>
科目: 来源:2013-2014学年河南省高三年级12月月考文科数学试卷(解析版) 题型:选择题
已知不共线向量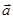 ,
,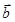 ,|
,|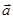 |=2,|
|=2,|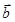 |=3,
|=3,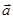 ·(
·(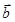 -
-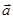 )=1,则|
)=1,则|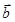 -
-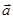 |=( )
|=( )
A.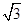 B.2
B.2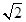 C.
C.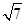 D.
D.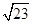
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com