
科目: 来源:2014届湖南省四校高三上学期第三次联考理科数学试卷(解析版) 题型:填空题
函数 的定义域为D,若存在闭区间[a,b]
的定义域为D,若存在闭区间[a,b] D,使得函数
D,使得函数 满足:(1)
满足:(1) 在[a,b]内是单调函数;(2)
在[a,b]内是单调函数;(2) 在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=
在[a,b]上的值域为[2a,2b],则称区间[a,b]为y= 的“美丽区间”.下列函数中存在“美丽区间”的是
. (只需填符合题意的函数序号)
的“美丽区间”.下列函数中存在“美丽区间”的是
. (只需填符合题意的函数序号)
①、 ; ②、
; ②、 ;
;
③、 ; ④、
; ④、 .
.
查看答案和解析>>
科目: 来源:2014届湖南省四校高三上学期第三次联考理科数学试卷(解析版) 题型:解答题
已知函数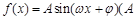 >0,
>0,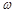 >0,
>0,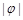 <
<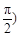 的图像与
的图像与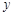 轴的交点为(0,1),它在
轴的交点为(0,1),它在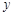 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为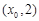 和
和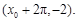
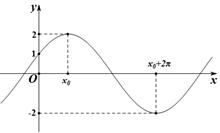
(1)求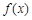 的解析式及
的解析式及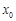 的值;
的值;
(2)若锐角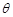 满足
满足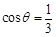 ,求
,求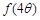 的值.
的值.
查看答案和解析>>
科目: 来源:2014届湖南省四校高三上学期第三次联考理科数学试卷(解析版) 题型:解答题
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为 立方米,且
立方米,且 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为 千元.
千元.

(Ⅰ)写出 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的 .
.
查看答案和解析>>
科目: 来源:2014届湖南省四校高三上学期第三次联考理科数学试卷(解析版) 题型:解答题
已知函数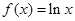 ,
,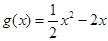 .
.
(Ⅰ)设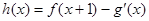 (其中
(其中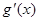 是
是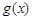 的导函数),求
的导函数),求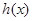 的最大值;
的最大值;
(Ⅱ)求证:当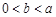 时,有
时,有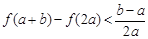 ;
;
(Ⅲ)设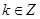 ,当
,当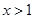 时,不等式
时,不等式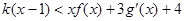 恒成立,求
恒成立,求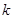 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com