
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:填空题
将含有3n个正整数的集合M分成元素个数相等且两两没有公共元素的三个集合A、B、C,其
中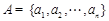 ,
,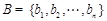 ,
,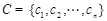 ,若A、B、C中的元素满足条件:
,若A、B、C中的元素满足条件: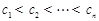 ,
,
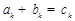 ,
,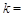 1,2,…,
1,2,…,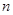 ,则称
,则称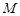 为“完并集合”.
为“完并集合”.
(1)若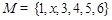 为“完并集合”,则
为“完并集合”,则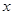 的一个可能值为
.(写出一个即可)
的一个可能值为
.(写出一个即可)
(2)对于“完并集合”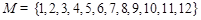 ,在所有符合条件的集合
,在所有符合条件的集合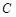 中,其元素乘积最小的集合是
.
中,其元素乘积最小的集合是
.
查看答案和解析>>
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:填空题
在直角坐标系 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴
轴的正半轴
为极轴建立极坐标系.曲线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,则
,则 与
与 交点在直角坐标系中的坐标为 ____.
交点在直角坐标系中的坐标为 ____.
查看答案和解析>>
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:解答题
已知函数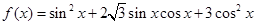 ,
,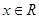 .求:
.求:
(I)求函数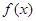 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(II)求函数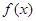 在区间
在区间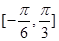 上的值域.
上的值域.
查看答案和解析>>
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:解答题
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是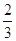 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
查看答案和解析>>
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:解答题
如图,四棱柱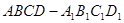 的底面
的底面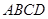 是平行四边形,且
是平行四边形,且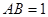 ,
,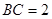 ,
,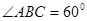 ,
,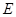 为
为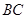 的中点,
的中点,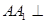 平面
平面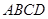 .
.
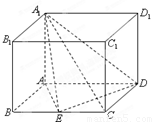
(Ⅰ)证明:平面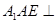 平面
平面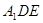 ;
;
(Ⅱ)若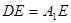 ,试求异面直线
,试求异面直线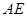 与
与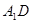 所成角的余弦值;
所成角的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试求二面角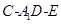 的余弦值.
的余弦值.
查看答案和解析>>
科目: 来源:2014届广东省广州市高三9月三校联考理科数学试卷(解析版) 题型:解答题
已知椭圆 的两个焦点
的两个焦点 和上下两个顶点
和上下两个顶点 是一个边长为2且∠F1B1F2为
是一个边长为2且∠F1B1F2为 的菱形的四个顶点.
的菱形的四个顶点.
(1)求椭圆 的方程;
的方程;
(2)过右焦点F2
,斜率为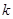 (
(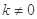 )的直线
)的直线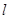 与椭圆
与椭圆 相交于
相交于 两点,A为椭圆的右顶点,直线
两点,A为椭圆的右顶点,直线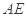 、
、 分别交直线
分别交直线 于点
于点 、
、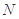 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 .求证:
.求证: 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com