
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
设命题p:函数 的定义域为R;命题q:
的定义域为R;命题q: 对一切的实数
对一切的实数 恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
设函数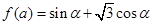 ,其中,角
,其中,角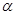 的顶点与坐标原点重合,始边与
的顶点与坐标原点重合,始边与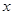 轴非负半轴重合,终边经过点
轴非负半轴重合,终边经过点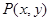 ,且
,且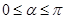 .
.
(1)若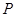 点的坐标为(-
点的坐标为(-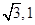 ),求
),求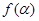 的值;
的值;
(2)若点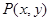 为平面区域
为平面区域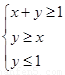 上的一个动点,试确定角
上的一个动点,试确定角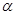 的取值范围,并求函数
的取值范围,并求函数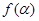 的值域.
的值域.
查看答案和解析>>
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品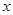 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为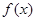 万元,且
万元,且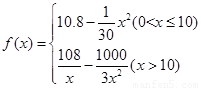
(1)写出年利润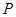 (万元)关于年产品
(万元)关于年产品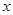 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
若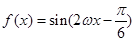 的图象关于直线
的图象关于直线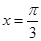 对称,其中
对称,其中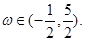
(1)求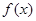 的解析式;
的解析式;
(2)将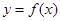 的图象向左平移
的图象向左平移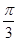 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到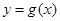 的图象;若函数
的图象;若函数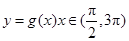 的图象与
的图象与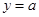 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求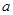 的值.
的值.
查看答案和解析>>
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
定议在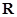 上的单调函数
上的单调函数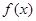 满足
满足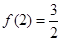 ,且对任意
,且对任意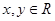 都有
都有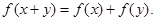
(1)求证: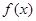 为奇函数;
为奇函数;
(2)若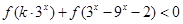 对任意
对任意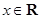 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源:2014届山东省高三10月份阶段检测理科数学试卷(解析版) 题型:解答题
已知函数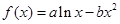 图象上一点
图象上一点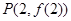 处的切线方程为
处的切线方程为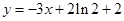 .
.
(1)求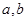 的值;
的值;
(2)若方程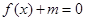 在
在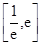 内有两个不等实根,求
内有两个不等实根,求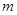 的取值范围(其中
的取值范围(其中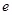 为自然对数的底数);(3)令
为自然对数的底数);(3)令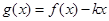 ,若
,若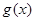 的图象与
的图象与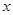 轴交于
轴交于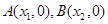 (其中
(其中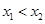 ),
),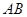 的中点为
的中点为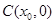 ,求证:
,求证: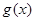 在
在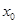 处的导数
处的导数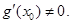
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com