相关习题
0 74709 74717 74723 74727 74733 74735 74739 74745 74747 74753 74759 74763 74765 74769 74775 74777 74783 74787 74789 74793 74795 74799 74801 74803 74804 74805 74807 74808 74809 74811 74813 74817 74819 74823 74825 74829 74835 74837 74843 74847 74849 74853 74859 74865 74867 74873 74877 74879 74885 74889 74895 74903 266669
科目:
来源:2012-2013学年广东省湛江二中高二(上)期中数学试卷(解析版)
题型:解答题
某市一公交线路某区间内共设置六个站点,分别为A,A1,A2,A3,A4,A5,现有甲乙两人同时从A站点上车,且他们中的每个人在站点Ai(i=1,2,3,4,5)下车是等可能的.
(Ⅰ)求甲在A2站点下车的概率;
(Ⅱ)甲,乙两人不在同一站点下车的概率.
查看答案和解析>>
科目:
来源:2012-2013学年广东省湛江二中高二(上)期中数学试卷(解析版)
题型:解答题
设数列{a
n}的前项n和为S
n,点
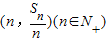
均在函数y=2x-1的图象上.
(1)求数列{a
n}的通项公式;
(2)设
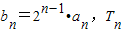
是数列{b
n}的前n项和,求T
n.
查看答案和解析>>
科目:
来源:2012-2013学年广东省湛江二中高二(上)期中数学试卷(解析版)
题型:解答题
已知圆C:x2+y2-2x-2y+1=0,直线l经过点P(0,-2)
(1)当直线l与圆相切时,求此时直线l的方程;
(2)已知点M在圆C上运动,求点M到直线l的距离的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:
来源:2012-2013学年广东省湛江二中高二(上)期中数学试卷(解析版)
题型:解答题
(文)已知函数
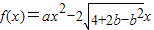
,
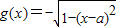
,(a,b∈R)
(Ⅰ)当b=0时,若f(x)在[2,+∞)上单调递增,求a的取值范围;
(Ⅱ)求满足下列条件的所有实数对(a,b):当a是整数时,存在x
,使得f(x
)是f(x)的最大值,g(x
)是g(x)的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对(a,b),试构造一个定义在D={x|x>-2,且x≠2k-2,k∈N}上的函数h(x),使当x∈(-2,0)时,h(x)=f(x),当x∈D时,h(x)取得最大值的自变量的值构成以x
为首项的等差数列.
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
设集合M={y|y=x2+1,x∈R},N={y|y=x+1,x∈R},则M∩N=( )
A.(0,1),(1,2)
B.{(0,1),(1,2)}
C.{y|y=1或y=2}
D.{y|y≥1}
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
已知f(x)=
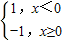
,则f(f(2))=( )
A.-2
B.-1
C.1
D.2
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
下列命题错误的是( )
A.“x>2”是“x2-3x+2>0”的充分不必要条件
B.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x=1,则x2-3x+2≠0”
C.对命题:“对”k>0,方程x2+x-k=0有实根”的否定是:“?k>0,方程x2+x-k=0无实根”
D.若命题P:x∈A∪B,则-P是x∉A且x∉B
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
设l,m是两条不同的直线,α是一个平面,则下列命题正确的是( )
A.若l⊥α,m⊥α,则l∥m
B.若m⊥l,l?α,则m⊥α
C.若m∥l,l∥α,则m∥α
D.若l⊥m,m⊥α,则l∥α
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
设

,

是单位向量,则“

•

=1”是“

=

”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:
来源:2012-2013学年浙江省金华市东阳市南马高中高三(上)期中数学试卷(解析版)
题型:选择题
如图,若某几何体的正视图、侧视图、俯视图均为直角三角形,则这个几何体的表面中,直角三角形的个数为( )

A.1
B.2
C.3
D.4
查看答案和解析>>

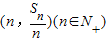 均在函数y=2x-1的图象上.
均在函数y=2x-1的图象上.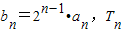 是数列{bn}的前n项和,求Tn.
是数列{bn}的前n项和,求Tn.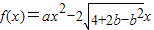 ,
,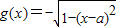 ,(a,b∈R)
,(a,b∈R) ,
, 是单位向量,则“
是单位向量,则“ •
• =1”是“
=1”是“ =
= ”的( )
”的( )