相关习题
0 76214 76222 76228 76232 76238 76240 76244 76250 76252 76258 76264 76268 76270 76274 76280 76282 76288 76292 76294 76298 76300 76304 76306 76308 76309 76310 76312 76313 76314 76316 76318 76322 76324 76328 76330 76334 76340 76342 76348 76352 76354 76358 76364 76370 76372 76378 76382 76384 76390 76394 76400 76408 266669
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
在平面直角坐标系xOy中,过坐标原点的一条直线与函数
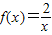
的图象交于P、Q两点,则线段PQ长的最小值是
.
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
函数f(x)的定义域为A,若x
1,x
2∈A且f(x
1)=f(x
2)时总有x
1=x
2,则称f(x)为单函数,例如,函数f(x)=2x+1(x∈R)是单函数.下列命题:
①函数f(x)=x
2(x∈R)是单函数;
②函数
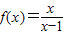
是单函数;
③若f(x)为单函数,x
1,x
2∈A且x
1≠x
2,,则f(x
1)≠f(x
2);
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是
.(写出所有真命题的编号)
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
在极坐标系中,点

到圆ρ=2cosθ的圆心的距离是
.

查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:填空题
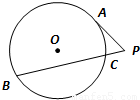
如图,⊙O的半径R=5,P是弦BC延长线上的一点,过P点作⊙O的切线,切点为A,若PC=1,PA=3,则圆心O到弦BC的距离是
.
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知α为锐角,且tanα=

.求
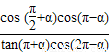
的值.
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设全集为R,集合
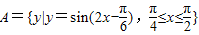
,集合B={a∈R|关于x的方程x
2+ax+1=0的根一个在(0,1)内,另一个在(1,2)内}.求(C
RA)∩(C
RB).
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
设函数
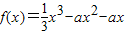
,g(x)=2x
2+4x+c.
(1)试问函数f(x)能否在x=-1时取得极值?说明理由;
(2)若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图象有两个公共点,求c的取值范围.
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20≤x≤200时,车流速度v是车流密度x的一次函数.
(I)当0≤x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)f(x)=x•v(x)可以达到最大,并求出最大值.(精确到1辆/小时).
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m使得f(cos2θ-3)+f(4m-2mcosθ)>f(0),对一切
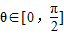
都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年广东省肇庆市高要二中高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=
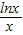
的图象为曲线C,函数g(x)=

ax+b的图象为直线l.
(1)当a=2,b=-3时,求F(x)=f(x)-g(x)的最大值;
(2)设直线l与曲线C的交点的横坐标分别为x
1,x
2,且x
1≠x
2,求证:(x
1+x
2)g(x
1+x
2)>2.
查看答案和解析>>

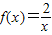 的图象交于P、Q两点,则线段PQ长的最小值是 .
的图象交于P、Q两点,则线段PQ长的最小值是 .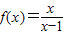 是单函数;
是单函数;
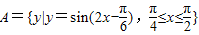 ,集合B={a∈R|关于x的方程x2+ax+1=0的根一个在(0,1)内,另一个在(1,2)内}.求(CRA)∩(CRB).
,集合B={a∈R|关于x的方程x2+ax+1=0的根一个在(0,1)内,另一个在(1,2)内}.求(CRA)∩(CRB).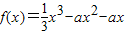 ,g(x)=2x2+4x+c.
,g(x)=2x2+4x+c.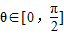 都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.
都成立?若存在,求出实数m的取值范围;若不存在,请说明理由.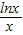 的图象为曲线C,函数g(x)=
的图象为曲线C,函数g(x)= ax+b的图象为直线l.
ax+b的图象为直线l.