相关习题
0 76374 76382 76388 76392 76398 76400 76404 76410 76412 76418 76424 76428 76430 76434 76440 76442 76448 76452 76454 76458 76460 76464 76466 76468 76469 76470 76472 76473 76474 76476 76478 76482 76484 76488 76490 76494 76500 76502 76508 76512 76514 76518 76524 76530 76532 76538 76542 76544 76550 76554 76560 76568 266669
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:填空题
定义在[-4,4]上的偶函数f(x)在区间[0,4]上单调递减,若f(1-m)<f(m),则实数m的取值范围是 .
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:填空题
已知存在实数a,满足对任意的实数b,直线y=-x+b都不是曲线y=x3-3ax的切线,则实数a的取值范围是 .
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:填空题
已知函数f (x)=ax
2+bx+

与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f (x-t)≤x恒成立,则所有满足条件的实数t的值为
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:填空题
函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[-b,-a],那么y=f(x)叫做对称函数,现有f(x)=
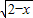
-k是对称函数,那么k的取值范围是
.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
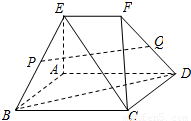
如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与面ABCD垂直,且AE⊥AD,EF∥AD,其中P,Q分别为棱BE,DF的中点.
(1)求证:BD⊥CE;
(2)求证:PQ∥平面ABCD.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
设等差数列{a
n}的前n项和为S
n,且a
5+a
13=34,S
3=9.
(1)求数列{a
n}的通项公式及前n项和公式;
(2)设数列{b
n}的通项公式为
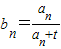
,问:是否存在正整数t,使得b
1,b
2,b
m(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
已知椭圆E:

的左顶点为A,左、右焦点分别为F
1、F
2,且圆C:

过A,F
2两点.
(1)求椭圆E的方程;
(2)设直线PF
2的倾斜角为α,直线PF
1的倾斜角为β,当β-α=

时,证明:点P在一定圆上.
(3)直线BC过坐标原点,与椭圆E相交于B,C,点Q为椭圆E上的一点,若直线QB,QC的斜率k
QB,k
QC存在且不为0,求证:k
QB•k
QC为定植.
查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
如图是一块长方形区域ABCD,AD=2(km),AB=1(km).在边AD的中点O处,有一个可转动的探照灯,其照射角∠EOF始终为

,设∠AOE=α(0≤α≤

),探照灯O照射在长方形ABCD内部区域的面积为S.
(1)当0≤α<

时,写出S关于α的函数表达式;
(2)当0≤α≤

时,求S的最大值.
(3)若探照灯每9分钟旋转“一个来回”(OE自OA转到OC,再回到OA,称“一个来回”,忽略OE在OA及OC反向旋转时所用时间),且转动的角速度大小一定,设AB边上有一点G,且∠AOG=

,求点G在“一个来回”中,被照到的时间.

查看答案和解析>>
科目:
来源:2012-2013学年江苏省盐城市东台市安丰中学高三(上)期中数学试卷(解析版)
题型:解答题
已知

.
(1)若函数f(x)在区间(a,a+1)上有极值,求实数a的取值范围;
(2)若关于x的方程f(x)=x
2-2x+k有实数解,求实数k的取值范围;
(3)当n∈N*,n≥2时,求证:

.
查看答案和解析>>

 与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f (x-t)≤x恒成立,则所有满足条件的实数t的值为 .
与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f (x-t)≤x恒成立,则所有满足条件的实数t的值为 .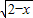 -k是对称函数,那么k的取值范围是 .
-k是对称函数,那么k的取值范围是 .
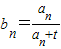 ,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由.
,问:是否存在正整数t,使得b1,b2,bm(m≥3,m∈N)成等差数列?若存在,求出t和m的值;若不存在,请说明理由. 的左顶点为A,左、右焦点分别为F1、F2,且圆C:
的左顶点为A,左、右焦点分别为F1、F2,且圆C: 过A,F2两点.
过A,F2两点. 时,证明:点P在一定圆上.
时,证明:点P在一定圆上. ,设∠AOE=α(0≤α≤
,设∠AOE=α(0≤α≤ ),探照灯O照射在长方形ABCD内部区域的面积为S.
),探照灯O照射在长方形ABCD内部区域的面积为S. 时,写出S关于α的函数表达式;
时,写出S关于α的函数表达式; 时,求S的最大值.
时,求S的最大值. ,求点G在“一个来回”中,被照到的时间.
,求点G在“一个来回”中,被照到的时间.
 .
. .
.