
已知在![]() ABC中,
ABC中,![]() 边BC的长与BC边上的高的和为20.
边BC的长与BC边上的高的和为20.
⑴写出![]() ABC的面积
ABC的面积![]() 与BC的长
与BC的长![]() 之间的函数关系式,并求出面积为48时BC的长;
之间的函数关系式,并求出面积为48时BC的长;
⑵当BC多长时,![]() ABC的面积最大?最大面积是多少?
ABC的面积最大?最大面积是多少?
⑶当![]() ABC面积最大时,是否存在其周长最小的情形?如果存在,请说明理由,并求出其最小周长;如果不存在,请给予说明.
ABC面积最大时,是否存在其周长最小的情形?如果存在,请说明理由,并求出其最小周长;如果不存在,请给予说明.
【解析】⑴依题意得:![]() ,
,
解方程![]() 得:
得:![]() ,∴当
,∴当![]() ABC面积为48时BC的长为12 或8;
ABC面积为48时BC的长为12 或8;
 ⑵ 由⑴得:
⑵ 由⑴得:![]() ,
,
∴当![]() 即BC=10时,
即BC=10时,![]() ABC的面积最大,最大面积是50;
ABC的面积最大,最大面积是50;
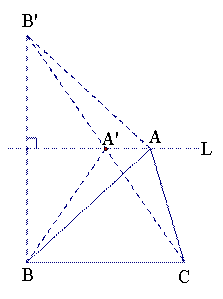
⑶![]() ABC的周长存在最小的情形,理由如下:
ABC的周长存在最小的情形,理由如下:
由⑵可知![]() ABC的面积最大时,BC=10,BC边上的高也为10,
ABC的面积最大时,BC=10,BC边上的高也为10,
过点A作直线L平行于BC,作点B关于直线L的对称点![]() ,
,
连接![]() 交直线L于点
交直线L于点![]() ,再连接
,再连接![]() ,
,
则由对称性得:![]() ,
,
∴![]() ,
,
当点A不在线段![]() 上时,则由三角形三边关系可得:
上时,则由三角形三边关系可得:
![]() ,
,
当点A在线段![]() 上时,即点A与
上时,即点A与![]() 重合,这时
重合,这时![]() ,
,
因此当点A与![]() 重合时,
重合时,![]() ABC的周长最小;
ABC的周长最小;
这时由作法可知:![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
因此当![]() ABC面积最大时,存在其周长最小的情形,最小周长为
ABC面积最大时,存在其周长最小的情形,最小周长为![]() .
.


科目:初中数学 来源: 题型:
 (2013•浦东新区一模)如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于( )
(2013•浦东新区一模)如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于( )查看答案和解析>>
科目:初中数学 来源:2013年山东省聊城市高级中等学校招生考试数学 题型:044
已知在△ABC中,边BC的长与BC边上的高的和为20.
(1)写出△ABC的面积y与BC的长x之间的函数关系式,并求出面积为48时BC的长;
(2)当BC多长时,△ABC的面积最大?最大面积是多少?
(3)当△ABC面积最大时,是否存在其周长最小的情形?如果存在,请说明理由,并求出其最小周长;如果不存在,请给予说明.
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
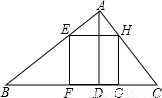
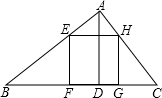 如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于
如图,已知在△ABC中,边BC=6,高AD=3,正方形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,那么这个正方形的边长等于查看答案和解析>>
科目:初中数学 来源:2013年上海市浦东新区中考数学一模试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com