
【题目】如图,在长方形ABCD中,AB=CD=8cm,BC=14cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:

(1)BP= cm(用t的代数式表示)
(2)当t为何值时,![]() ABP
ABP![]() DCP?
DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得![]() ABP与
ABP与![]() PQC全等?若存在,请求出v的值;若不存在,请说明理由。
PQC全等?若存在,请求出v的值;若不存在,请说明理由。
【答案】(1)BP=2t;(2)t=![]() ;(3)当v=2或
;(3)当v=2或![]() 时,△ABP与△PQC全等.
时,△ABP与△PQC全等.
【解析】
(1)根据P点的运动速度可得BP的长;
(2)根据全等三角形的性质即可得出BP=CP即可;
(3)此题主要分两种情况①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t.
(2)当t=![]() 时,△ABP≌△DCP,
时,△ABP≌△DCP,
理由:∵BP=2t,CP=142t,
∵△ABP≌△DCP,
∴BP=CP,
∴2t=142t,
∴t=![]() .
.
(3)①当△ABP≌△PCQ时,
∴BP=CQ,AB=PC,
∵AB=8,
∴PC=8,
∴BP=BCPC=148=6,
2t=6,
解得:t=3,
CQ=BP=6,
v×3=6,
解得:v=2;
②当△ABP≌△QCP时,
∴BA=CQ,PB=PC
∵PB=PC,
∴BP=PC=![]() BC=7,
BC=7,
2t=7,
解得:t=![]() ,
,
CQ=BA=8,
v×![]() =8,
=8,
解得:v=![]() .
.
综上所述:当v=2或![]() 时,△ABP与△PQC全等.
时,△ABP与△PQC全等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,画![]() ,并画
,并画![]() 的平分线
的平分线![]() .
.
(1)将三角尺的直角顶点落在![]() 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与![]() 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则![]()
![]() (选填<,>,=)
(选填<,>,=)

(2)把三角尺绕着点P旋转(如图2),![]() 与
与![]() 相等吗?试猜想
相等吗?试猜想![]() 、
、![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
拓展延伸1:在(2)条件下,过点P作直线![]() ,分别交
,分别交![]() 、
、![]() 于点G、H,如图3
于点G、H,如图3
①图中全等三角形有多少对(不添加辅助线)
②猜想![]() 、
、![]() 、
、![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.
拓展延伸2:
画![]() ,并画
,并画![]() 的平分线
的平分线![]() ,在
,在![]() 上任取一点P,作
上任取一点P,作![]() .
.![]() 的两边分别与
的两边分别与![]() 、
、![]() 相交于E、F两点(如图4),
相交于E、F两点(如图4),![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四组条件中,无法判定△ABC≌△DEF的是( )
A. AB=DE,BC=EF,∠B=∠EB. ∠B=∠E,BC=EF,∠C=∠F
C. ∠B=∠E,∠A=∠D,BC=EFD. AB=DE,BC=EF,∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
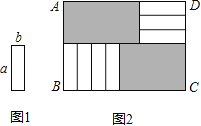
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
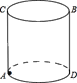
【题目】如图,圆柱的高为![]() ,底面半径为
,底面半径为![]() ,在圆柱下底面的
,在圆柱下底面的![]() 点处有一只蚂蚁,它想吃到上底面
点处有一只蚂蚁,它想吃到上底面![]() 处的食物,已知四边形
处的食物,已知四边形![]() 的边
的边![]() 、
、![]() 恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
恰好是上、下底面的直径.为:蚂蚁至少要爬行多少路程才能食到食物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com