解:(1)∵a,b是方程|x+9|=1的两根(a<b),
解得:a=-10,b=-8,
∵(c-16)
2与|d-20|互为相反数,
∵(c-16)
2≥0,|d-20|≥0,
∴c-16=0,d-20=0,
可得:c=16,d=20;
(2)经时间t时,A的值为6t-10,B的值为6t-8,
C的值为16-2t,D的值为20-2t,
要使A、B两点都运动在线段CD上,
则必须满足条件:A在C的右侧,B在D的左侧,
列出不等式:
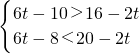
,
解得:

<t<

,
故t的范围是:

<t<

.
(3)①点A运动到点D的左边,点B运动到点D的右边,此时

<t≤

,
A的值为6t-10,B的值为6t-8,C的值为16-2t,D的值为20-2t,
AD=20-2t-(6t-10)=30-8t,BC=6t-8-(16-2t)=8t-24,
由题意得:8t-24=4(30-8t),
解得:t=

,
∵

<t≤

,
∴t不存在.
②点A、点B均在点D的右边,此时t>

,
A的值为6t-10,B的值为6t-8,C的值为16-2t,D的值为20-2t,
AD=6t-10-(20-2t)=8t-30,BC=6t-8-(16-2t)=8t-24,
由题意得,8t-24=4(8t-30),
解得:t=4,满足t>

;
综上可得存在时间t=4,使B与C的距离是A与D的距离的4倍.
分析:(1)根据非负数的性质,及相反数的定义,可得出a、b、c、d的值;
(2)要使A、B两点都运动在线段CD上,则必须满足条件:A在C的右侧,B在D的左侧,由此可得出t的范围;
(3)分两种情况,①点A运动到点D的左边,点B运动到点D的右边,②点A、点B均在点D的右边,然后分别表示出BC、AD的长度,建立方程,求解即可.
点评:本题考查了一元一次方程的应用,涉及了动点问题的计算,解答本题关键是表示出运动后四个点的坐标,注意分类讨论思想的运用,难度较大.

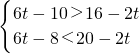 ,
, <t<
<t< ,
, <t<
<t< .
. <t≤
<t≤ ,
, ,
, <t≤
<t≤ ,
, ,
, ;
;

 同步练习强化拓展系列答案
同步练习强化拓展系列答案 5、如图,数轴上有A,B,C,D,E,P六个点,已知AB=BC=CP=PD=DE,且A点表示-5,E点表示9,则下列四个整数中,P点最接近的是( )
5、如图,数轴上有A,B,C,D,E,P六个点,已知AB=BC=CP=PD=DE,且A点表示-5,E点表示9,则下列四个整数中,P点最接近的是( )