
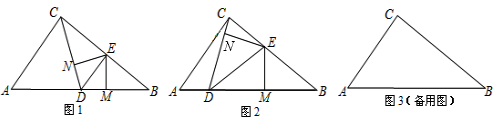
如图①,在Rt△ABC中,∠BAC=90°,AB=AC=![]() ,D、E两点分别在AC、BC上,且DE∥AB,CD=
,D、E两点分别在AC、BC上,且DE∥AB,CD=![]() .将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、 E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.
.将△CDE绕点C顺时针旋转,得到△CD’E’(如图②,点D’、 E’分别与点D、E对应),点E’在AB上,D’E’与AC相交于点M.
(1)求∠ACE’的度数;
(2)求证:四边形ABCD’是梯形;
(3)求△AD’M的面积.

解:(1)∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°.
∵DE//AB,∴∠DEC= ∠DCE=45°,∠EDC=90°,
∵DE=CD=2![]() ,∴CE=CE‘=4.
,∴CE=CE‘=4.
在Rt△ACE’中,∠E’AC=90°,AC=2![]() ,CE ‘=4,
,CE ‘=4,
∴cos∠ACE’=![]() ,∴∠ACE’=30。
,∴∠ACE’=30。
(2)∵∠D’CE=∠ACB=45°,∠ACE’=30°.∠D’CA=∠E’CB=15°.
又![]() ,∴△D‘CA∽△E’CB.
,∴△D‘CA∽△E’CB.
∴∠D’AC=∠B=45°.∴∠ACB=∠D’AC.
∴AD’//BC.∴∠B=45°,∠D’CB=60°,
∴∠ABC与∠D’CB不互补,
∴AB与D’C不平行.∴四边形ABCD ‘是梯形.
(3)如图,过点C作CF⊥AD’,垂足为F’.∵AD’∥BC,∴CF⊥BC.

∴∠FCD’=∠ACF一∠ACD’=30°.
在Rt△ACF中,AF=CF=![]() ,∴S△ACF=3.
,∴S△ACF=3.
在Rt△D’CF中, CD’=2![]() ,∠FCD’=30°,∴D’F=
,∠FCD’=30°,∴D’F=![]() ,∴S△D’CF=
,∴S△D’CF=![]() .
.
同理,SRt△AE’C=2![]() ,SRt△D’E’C=4.∵∠AME’=∠D’MC,∠E’AM=∠CD’M,
,SRt△D’E’C=4.∵∠AME’=∠D’MC,∠E’AM=∠CD’M,
∴△AME’∽△D’MC.∴ ,
,
∴ S△AE’M=![]() S△CD’M
S△CD’M
(1)∵S△E’MC+S△AE’M=S△AE’C=2![]() (2),S△E’MC+S△CD’M=S△DE’C=4
(2),S△E’MC+S△CD’M=S△DE’C=4
(3).(3)一(2),得S△CD’M-S△AE’M=4-2![]() .
.
由S△CD’M=8―4![]() .∴S△AD’M=S△ACF一S△D’CF―S△CD’M=3
.∴S△AD’M=S△ACF一S△D’CF―S△CD’M=3![]() 一5,
一5,
∴△AD’M的面积是3![]() 一5
一5


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com