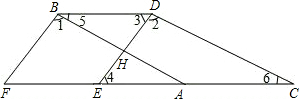
解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
又∵∠5=∠6,
∴∠BAF=∠6,
∴AB∥CD,
∴∠2=∠EHA,
又∵∠1=∠2,即∠1=∠EHA,
∴BF∥DE.
另解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
∵∠5=∠6,
∴∠BAF=∠6,
∵△BFA、△DEC的内角和都是180°
∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6
∵∠1=∠2;∠BAF=∠6
∴∠BFA=∠4(同位角相等,两直线就平行)
∴BF∥DE.
分析:设AB与DE相交于H,若判断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.
点评:解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.

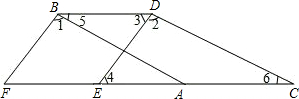 如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么. 解:BF、DE互相平行;
解:BF、DE互相平行;

 =2,∠ADC=30°
=2,∠ADC=30°