练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】学校组织学生参加知识问答，问答活动共设有20道选择题，各题分值相同，每题必答，下表记录了A、B、C三名学生的得分情况，则参赛学生D的得分可能是（　　）

    参赛学生

    答对题数

    答错题数

    得分

    A

    20

    0

    100

    B

    19

    1

    94

    C

    14

    6

    64

    A.66B.93C.40D.87

    【答案】C

    【解析】

    根据表格中3名参赛学生的得分情况，可知答错一题扣6分，设参赛学生D答错x道题（0≤x≤20，且x为整数），则其得分值为：100﹣6x，然后逐个选项进行计算，结果符合x的取值范围的为正确答案．

    解：根据表格数据，A学生答对20道得分100，由B、C同学得分情况可知答错一题扣6分，

    故设参赛学生D答错x道题（0≤x≤20，且x为整数），则其得分值为：100﹣6x

    选项A：令100﹣6x＝66，解得x＝，故本选项不符合题意；

    选项B：令100﹣6x＝93，解得x＝，故本选项不符合题意；

    选项C：令100﹣6x＝40，解得x＝10，故本选项符合题意；

    选项D：令100﹣6x＝87，解得x＝，故本选项不符合题意．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：正方形ABCD的边长为8，点E、F分别在AD、CD上，AE＝DF＝2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了庆祝元旦，某商场在门前的空地上用花盆排列出了如图所示的图案，第1个图案中有10个花盆，第2个图案中有19个花盆，…，按此规律排列下去.

    （1）第3个图案中有______个花盆，第4个图案中有______个花盆；

    （2）根据上述规律，求出第个图案中花盆的个数（用含的代数式表示）；

    （3）是否存在恰好由2026个花盆排列出的具有上述规律的图案？若存在，说明它是第几个图案？若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

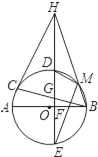
    【题目】如图，AB，BC分别是⊙O的直径和弦，点D为上一点，弦DE交⊙O于点E，交AB于点F，交BC于点G，过点C的切线交ED的延长线于H，且HC=HG，连接BH，交⊙O于点M，连接MD，ME．

    求证：

    （1）DE⊥AB；

    （2）∠HMD=∠MHE+∠MEH．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，O为直线AB上一点，OC为射线，∠AOC＝40°，将一个三角板的直角顶点放在点O处，一边OD在射线OA上，另一边OE与OC都在直线AB的上方．

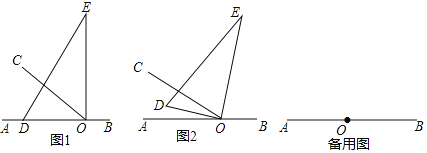
    （1）将三角板绕点O顺时针旋转，若OD恰好平分∠AOC（如图2），试说明OE平分∠BOC；

    （2）将三角板绕点O在直线AB上方顺时针旋转，当OD落在∠BOC内部，且∠COD＝∠BOE时，求∠AOE的度数：

    （3）将图1中的三角板和射线OC同时绕点O，分别以每秒6°和每秒2°的速度顺时针旋转一周，求第几秒时，OD恰好与OC在同一条直线上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是直线AB上任一点，射线OD和射线OE分别平分∠AOC和∠BOC．

    （1）填空：与∠AOE互补的角有　 　；

    （2）若∠COD＝30°，求∠DOE的度数；

    （3）当∠AOD＝α°时，请直接写出∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车配件加工厂给该厂的某车间下达了在一周内加工某种汽车配件 35000 件的任务，该车间接到任务后，计划平均每天加工 5000 件，由于各种原因，每天实际加工的件数与每天计划加工的件数相比有出入，把超额或不足的部分分别用正、负数来表示，下表是这周加工这种汽车配件的记录情况：

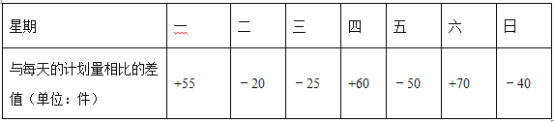
    （1）这周的前三天共加工了多少件？

    （2）这周内加工最多的一天比加工最少的一天多加工了多少件？

    （3）已知该厂对这个车间实行计件工资制，每加工 1 件得 12 元，若超额完成任务，则超额部分每件再奖 8 元；若没有完成任务，则每少一件倒扣 8 元，求该车间这周的总收入．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 为满足社区居民健身的需要，市政府准备采购若干套健身器材免费提供给社区，经考察，劲松公司有两种型号的健身器可供选择.

    （1）劲松公司2015年每套型健身器的售价为万元，经过连续两年降价，2017年每套售价为 万元，求每套型健身器年平均下降率 ；

    （2）2017年市政府经过招标，决定年内采购并安装劲松公司两种型号的健身器材共套，采购专项费总计不超过万元，采购合同规定：每套型健身器售价为万元，每套型健身器售价我 万元.

    ①型健身器最多可购买多少套？

    ②安装完成后，若每套型和型健身器一年的养护费分别是购买价的 和 .市政府计划支出 万元进行养护.问该计划支出能否满足一年的养护需要？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，过点的直线，为边上一点，过点作，交直线于点，垂足为点，连接.

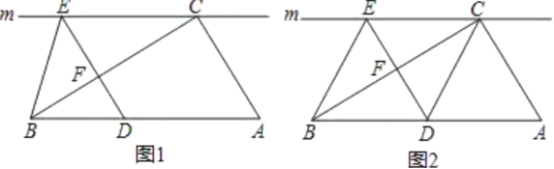
    （1）求证：；

    （2）如图，当点是中点时，连接.

    ①四边形是什么特殊四边形？说明你的理由；

    ②当 时，四边形是正方形.（直接写出答案）

    查看答案和解析>>

    同步练习册答案