
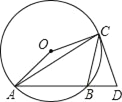
【题目】如图,点A、B、C均在⊙O上,过点C作⊙O的切线交AB的延长线于点D,∠ACB=45°,∠AOC=150°.
(1)求证:CD=CB;
(2)⊙O的半径为![]() ,求AC的长.
,求AC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)延长AO交⊙O于E点,连接CE,由题意可求∠E=75°,∠OAC=∠OCA=15°,∠OCD=90°,根据圆的内接四边形对角互补,以及三角形内角和定理可得∠D=∠CBD=75°,即可证CD=CB;
(2)连接OB,过点B作BF⊥AC于点F,由OA=OB,可得∠OAB=∠OBA=45°,即可求∠AOB=90°,根据勾股定理可求AB的长,AF的长,CF的长,即可求AC的长.
(1)证明:延长AO交⊙O于E点,连接CE
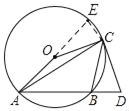
∵AE是直径
∴∠ACE=90°
∵∠ACB=45°
∴∠BCE=135°
∵AO=OC=EO,∠AOC=150°
∴∠OAC=∠OCA=15°,∠OEC=∠OCE=75°
∵四边形ABCE是圆内接四边形
∴∠EAB+∠ECB=180°,∠E+∠ABC=180°
∴∠EAB=45°,∠ABC=105°,
∴∠CAD=30°,∠CBD=75°
∵CD是⊙O切线,
∴∠OCD=90°
∵∠OCA=15°,∠ACB=45°
∴∠CBD=30°
∵∠D+∠CBD+∠BCD=180°
∴∠D=75°
∴∠D=∠CBD
∴CD=CB
(2)连接OB,过点B作BF⊥AC于点F,
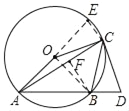
∵OA=OB
∴∠OAB=∠OBA=45°
∴∠AOB=90°
∴AB=![]() =2
=2
∵∠CAD=30°,BF⊥AC
∴BF=1,AF=![]() BF=
BF=![]()
∵∠ACB=45°,BF⊥AC
∴∠ACB=∠CBF=45°
∴CF=BF=1
∴AC=![]() +1
+1


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, ![]() :4棵;
:4棵; ![]() :5棵;
:5棵; ![]() :6棵;
:6棵; ![]() :7棵,将抽查结.果绘制成扇形图(如图1)和条形图(如图2).回答下列问题:
:7棵,将抽查结.果绘制成扇形图(如图1)和条形图(如图2).回答下列问题:
(1)在这次调查中![]() 类型有多少名学生?
类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目:初中数学 来源: 题型:
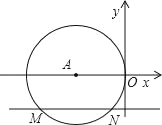
【题目】如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(﹣4,﹣2),则弦MN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为5,弦AB=6,P是AB上任意一点,点C是劣弧![]() 的中点,若△POC为直角三角形,则PB的长度( )
的中点,若△POC为直角三角形,则PB的长度( )
A. 1 B. 5 C. 1或5 D. 2或4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 角形与两坐标轴分别交于
角形与两坐标轴分别交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与直线
与直线![]() 交于点
交于点![]()
![]() 面积为
面积为![]() .
.
(1)求![]() 的值
的值
(2)直接写出不等式![]() 的解集;
的解集;
(3)点![]() 在
在![]() 上,如果
上,如果![]() 的面积为4,点
的面积为4,点![]() 的坐标.
的坐标.
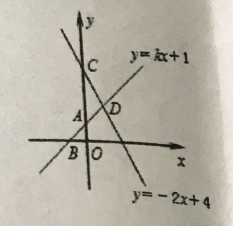
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崂山区某班全体同学参加了为一名因工受伤女教师捐款的活动,该班同学捐款情况的部分统计图如图所示:
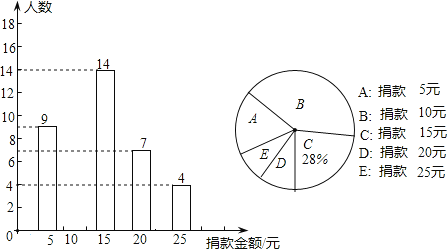
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款金额的众数;
(3)该班平均每人捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
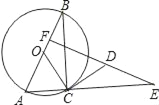
【题目】如图,⊙O是Rt△ABC的外接圆,AB为直径,∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点,ED⊥AB于F.
(1)判断△DCE的形状;
(2)设⊙O的半径为1,且OF=![]() ,求证:△DCE≌△OCB.
,求证:△DCE≌△OCB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com