
【题目】 如图,梯形ABCD中,BC∥AD,AB=AD,P为边AB上一点,连PC,PD,CD垂直于CP且∠CPD=∠A,BC=4BP,则![]() =_____.
=_____.
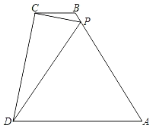
【答案】![]()
【解析】
过点C作CF⊥AB交AB的延长线于点F,在AF的延长线上截取EF=BF,连接CE,设∠A=∠CPD=α,先证△ECP∽△APD,可得![]() ,在Rt△CDP中,
,在Rt△CDP中,![]() =cosα,设BP=a,AD=b,EF=x,进而可得
=cosα,设BP=a,AD=b,EF=x,进而可得![]() ,由此计算即可得到答案.
,由此计算即可得到答案.
解:过点C作CF⊥AB交AB的延长线于点F,在AF的延长线上截取EF=BF,连接CE,设∠A=∠CPD=α,
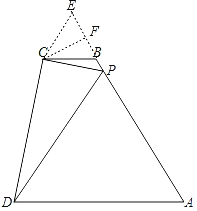
则CE=BC,
∴∠CEB=∠CBE,
∵BC∥AD,
∴∠A=∠CBE,
∴∠A=∠CEB=∠CPD=α,
∴∠CPE+∠DPA=180°﹣α,
又∵∠PDA+∠DPA=180°﹣α,
∴∠CPE=∠PDA,
∴△ECP∽△APD,
∴![]() ,
,
在Rt△CDP中,![]() =cosα,
=cosα,
∴![]() =cosα=
=cosα=![]() ,
,
设BP=a,AD=b,EF=x,
∵BC=4BP,AB=AD,
∴CE=BC=4a,PA=b﹣a,
∴![]() ,
,
解得:3b=31a,
∴cosα=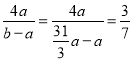 .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在一个不透明的小布袋中装有4个质地、大小完全相同的小球,它们分别标有数字0,1,2,3,小明从布袋里随机摸出一个小球,记下数字为![]() ,小红在剩下的3个小球中随机摸出一个小球,记下数字为
,小红在剩下的3个小球中随机摸出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)画树状图或列表,写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)小明和小红约定做一个游戏,其规则为:若![]() 在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
在第一象限,则小明胜;否则,小红胜;这个游戏公平吗?请你作出判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践活动课中小明同学测量某建筑物![]() 的高度,如图,已知斜坡
的高度,如图,已知斜坡![]() 的坡度为
的坡度为![]() ,小明在坡底点
,小明在坡底点![]() 处测得建筑物顶端
处测得建筑物顶端![]() 处的仰角为
处的仰角为![]() ,他沿着斜坡行走
,他沿着斜坡行走![]() 米到达点
米到达点![]() 处,在
处,在![]() 测得建筑 物顶端
测得建筑 物顶端![]() 处的仰角为
处的仰角为![]() ,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的
,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的![]() 高度约为( )(参考数据:
高度约为( )(参考数据:![]() )
)

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.
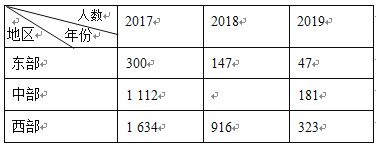
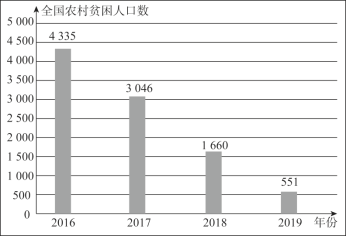
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是
A.2018年中部地区农村贫困人口为 597万人
B.2017-2019年,农村贫困人口数量都是东部最少
C.2016-2019年,农村贫困人口减少数量逐年增多
D.2017-2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程ax2+2x﹣3=0有两个不相等的实数根.
(1)求a的取值范围;
(2)若此方程的一个实数根为1,求a的值及方程的另一个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 交x轴负半轴于点A,交y轴于点C,抛物线
交x轴负半轴于点A,交y轴于点C,抛物线![]() 经过点A、C,与x轴的另一交点为B.
经过点A、C,与x轴的另一交点为B.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 设抛物线上任一动点P的横坐标为m.
设抛物线上任一动点P的横坐标为m.
①若点P在第二象限抛物线上运动,过P作![]() 轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
轴于点N交直线AC于点M,当直线AC把线段PN分成2:3两部分时,求m的值;
②连接CP,以点P为直角顶点作等腰直角三角形CPQ,当点Q落在抛物线的对称轴上时,请直接写出点P的坐标.
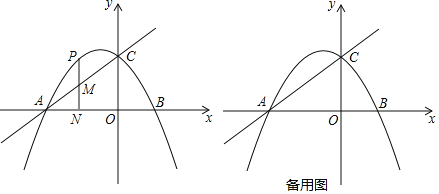
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com