
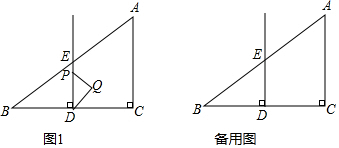
分析 (1)分两种情况进行讨论:点P在线段DE上,点P在DE的延长线上,根据线段的和差关系进行计算;
(2)当点Q落在边AC上时,过点Q作QF⊥DP于F,根据四边形CDFQ是矩形,△DPQ是等腰直角三角形,求得DP=2FQ=8,即可得到t的值;
(3)分两种情况进行讨论:①当点P在线段DE上时,△PDQ和△ABC重叠部分为△DPQ,②当点P在线段DE的延长线上时,△PDQ和△ABC重叠部分为四边形EDQG,分别求得S与t之间的函数关系式.
解答 解:(1)由题可得,DP=t,DE=$\frac{1}{2}$AC=3,
当点P在线段DE上时,EP=DE-DP=3-t;
当点P在DE的延长线上时,EP=DP-DE=t-3;
(2)如图所示,当点Q落在边AC上时,过点Q作QF⊥DP于F,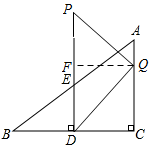
∵∠C=∠CDF=∠DFQ=90°,
∴四边形CDFQ是矩形,
∴FQ=CD=$\frac{1}{2}$BC=4,
∵△DPQ是等腰直角三角形,
∴DP=2FQ=8,
∴t=$\frac{8}{1}$=8(s);
(3)①当点P在线段DE上时,△PDQ和△ABC重叠部分为△DPQ,且DP=t,DP边上的高为$\frac{1}{2}$t,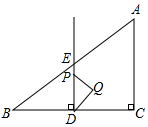
∵点P从点D运动到点E处时,时间为3s,
∴当0<t≤3时,S=$\frac{1}{2}$×t×$\frac{1}{2}$t=$\frac{1}{4}{t}^{2}$,
②当点P在线段DE的延长线上时,△PDQ和△ABC重叠部分为四边形EDQG,
如图所示,过G作GF⊥PE于F,则△GFE∽△BCA,且PF=GF,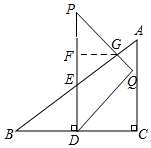
∵AC=6,BC=8,
∴EF:FG=3:4,EF:FP=3:4,
∵PE=t-3,
∴FG=$\frac{4}{7}$(t-3),
∴△PEG的面积=$\frac{1}{2}$×PE×FG=$\frac{1}{2}$×$\frac{4}{7}$(t-3)2,
由(2)可知,点Q落在边AC上时,t的值为8s,
∴当3≤t≤8时,S=$\frac{1}{4}$t2-$\frac{1}{2}$×$\frac{4}{7}$(t-3)2=-$\frac{1}{28}$t2+$\frac{12}{7}$t-$\frac{18}{7}$.
综上所述,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{\frac{1}{4}{t}^{2}(0<t≤3)}\\{-\frac{1}{28}{t}^{2}+\frac{12}{7}t-\frac{18}{7}(3≤t≤8)}\end{array}\right.$.
点评 本题属于三角形综合题,主要考查了等腰直角三角形的性质,相似三角形的判定与性质以及三角形面积的计算的综合应用,解决问题的关键是作辅助线构造直角三角形,解题时注意分类讨论思想的运用.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -$\frac{5}{3}$ | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由7x=4x-3移项得7x-4x=3 | |
| B. | 由$\frac{2x-1}{3}$=1+$\frac{x-3}{2}$去分母得2(2x-1)=1+3(x-3) | |
| C. | 由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1 | |
| D. | 由2(x+1)=x+7 移项、合并同类项得 x=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-33|<-32<(-3)2 | B. | |-33|<(-3)2<-32 | C. | -32<|-33|<(-3)2 | D. | -32<(-3)2<|-33| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com