练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

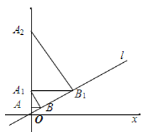
    【题目】如图，已知直线l：y=x，过点A(0，1)作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；……按此作法继续下去，则点A2020的坐标为______________．

    【答案】(0,)

    【解析】

    根据所给直线解析式可得l与x轴的夹角，进而根据所给条件依次得到点A1，A2，A3的坐标，通过相应规律得到A2020标即可．

    ∵直线l的解析式为：y=x

    ∴直线l与x轴的夹角为30°

    ∵AB∥x轴，

    ∴∠ABO=30°

    ∵OA=1，

    ∴AB =

    ∵A1B⊥l，

    ∴∠ABA1=60°

    ∴AA1=3，

    ∴A1(0,4)，

    同理可得A2(0,16)，A3(0,64)…，

    ∴A2020纵坐标为：42020，

    ∴A2020(0,42020)．

    故答案为：(0,)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

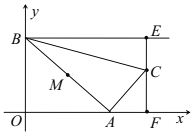
    【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠，使点A落在点Q处.

    (1)如图①，当点Q恰好落在OB上时.求点p的坐标；

    (2)如图②，当点P是AB中点时,直线OQ交BC于M点.

    ①求证:MB=MQ；②求点Q的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某县政府计划拨款34000元为福利院购买彩电和冰箱，已知商场彩电标价为2000元/台，冰箱标价为1800元/台，如按标价购买两种家电，恰好将拨款全部用完．

    （1）问原计划购买的彩电和冰箱各多少台？

    （2）购买的时候恰逢商场正在进行促销活动，全场家电均降价进行销售，若在不增加县政府实际负担的情况下，能否比原计划多购买3台冰箱？请通过计算回答．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点是轴非负半轴上的动点，点坐标为，是线段的中点，将点绕点顺时针方向旋转90°得到点，过点作轴的垂线，垂足为，过点作轴的垂线与直线相交于点，连接，，设点的横坐标为．

    （1）当时，求点的坐标；

    （2）设的面积为，当点在线段上时，求与之间的函数关系式，并写出自变量的取值范围；

    （3）当为何值时，取得最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=﹣x2﹣2x+3交x轴于点A、C（点A在点C左侧），交y轴于点B．

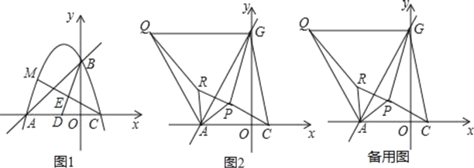
    （1）求A，B，C三点坐标；

    （2）如图1，点D为AC中点，点E在线段BD上，且BE=2DE，连接CE并延长交抛物线于点M，求点M坐标；

    （3）如图2，将直线AB绕点A按逆时针方向旋转15°后交y轴于点G，连接CG，点P为△ACG内一点，连接PA、PC、PG，分别以AP、AG为边，在它们的左侧作等边△APR和等边△AGQ，求PA+PC+PG的最小值，并求当PA+PC+PG取得最小值时点P的坐标（直接写出结果即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

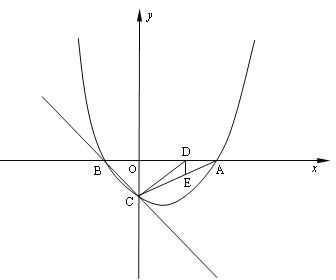
    【题目】如图, 已知抛物线与y轴相交于C，与x轴相交于A、B，点A的坐标为（2，0），点C的坐标为（0，-1）．

    （1）求抛物线的解析式；

    （2）点E是线段AC上一动点，过点E作DE⊥x轴于点D，连结DC，当△DCE的面积最大时，求点D的坐标；

    （3）在直线BC上是否存在一点P，使△ACP为等腰三角形，若存在，求点P的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，已知直线y=-2x+4与x轴、y轴分别交于点A、C，以OA、OC为边在第一象限内作长方形OABC．

    （1）求点A、C的坐标；

    （2）将△ABC对折，使得点A的与点C重合，折痕交AB于点D，求直线CD的解析式（图②）；

    （3）在坐标平面内，是否存在点P（除点B外），使得△APC与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

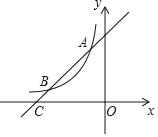
    【题目】如图，一次函数y＝x+4的图象与反比例函数y＝(k为常数且k≠0)的图象交于A(﹣1，a)，B两点，与x轴交于点C．

    (1)求a，k的值及点B的坐标；

    (2)若点P在x轴上，且S△ACP＝S△BOC，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

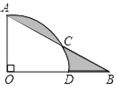
    【题目】如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点A、点C，交OB于点D，若OA＝3，则阴影都分的面积为___________．

    查看答案和解析>>

    同步练习册答案