
 如图两射线表示某电信公司提供两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,当通话时间为100分钟,两种方案通讯费用相差20元;当通话时间为180分钟,两种方案通讯费用一样;当两种方案通讯费用相差40元时,则通话时间为________分钟.
如图两射线表示某电信公司提供两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,当通话时间为100分钟,两种方案通讯费用相差20元;当通话时间为180分钟,两种方案通讯费用一样;当两种方案通讯费用相差40元时,则通话时间为________分钟. ,b=-45时或当k2-k1=-
,b=-45时或当k2-k1=- ,b=45时,分别求出即可.
,b=45时,分别求出即可.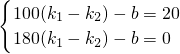 或
或 ,
, 或
或 ,
, ,b=-45时,
,b=-45时, )+45=40,
)+45=40, ,b=45时,
,b=45时, ,
, -45=40,
-45=40,

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com