
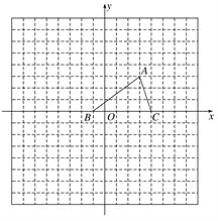
【题目】如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(-1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△A2B2C2.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线
轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线![]() ,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)计算甲队的平均成绩和方差;
(2)已知乙队成绩的方差是1分2 , 则成绩较为整齐的是哪一队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .则
.则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,线段
上的射影是________点,线段![]() 在
在![]() 上的射影是___,线段
上的射影是___,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
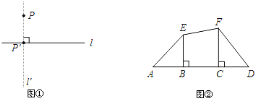
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AD=2AG;②GE:BE=1:3;③![]() ,其中正确的是( )
,其中正确的是( )

A. ①② B. ①②③ C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
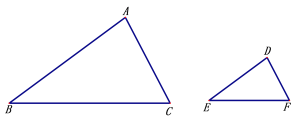
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
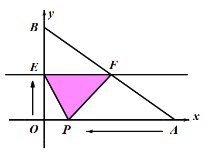
【题目】如图,已知A,B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个单位长度的速度向原点O运动,同时直线EF由x轴为起始位置以每秒1个单位长度的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E,F,连接EP,FP,设动点P与直线EF同时出发,运动时间为t秒.
(1)求t=15秒时,求EF的长度;
(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com