
【题目】“行千里,致广大”是重庆人民向大家发出的旅游邀请.如图,某建筑物上有一个旅游宣传语广告牌,小亮在![]() 处测得该广告牌顶部
处测得该广告牌顶部![]() 处的仰角为
处的仰角为![]() ,然后沿坡比为
,然后沿坡比为![]() 的斜坡
的斜坡![]() 行走
行走![]() 米至
米至![]() 处,在
处,在![]() 处测得广告牌底部
处测得广告牌底部![]() 处的仰角为
处的仰角为![]() ,已知
,已知![]() 与水平面
与水平面![]() 平行,
平行,![]() 与
与![]() 垂直,且
垂直,且![]() 米,则广告牌顶部
米,则广告牌顶部![]() 到
到![]() 的距离
的距离![]() 为( )(参考数据:
为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
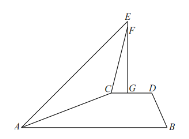
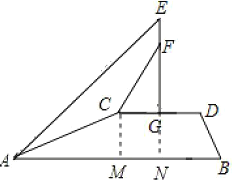
作CM⊥AB于M,延长EG交AB于N,根据矩形的性质得到GN=CM,MN=CG,根据坡度的概念求出AM、CM,根据等腰直角三角形的性质列式求出CG,结合图形计算即可.
作CM⊥AB于M,延长EG交AB于N,
则GN⊥AB,
∴四边形CMNG为矩形,
∴GN=CM,MN=CG,
斜坡AC的坡比为5:12,
则CM=5x,AM=12x,
由勾股定理得,(5x)2+(12x)2=652,
解得,x=5,
∴CM=5x=25,AM=12x=60,
在Rt△FCG中,tan∠FCG=![]() ,即
,即![]() =tan76°=4,
=tan76°=4,
∴FG=4CG,
∵∠EAN=45°,
∴AN=EN,即60+CG=2+4CG+25,
解得,CG=11,
∴FG=44,
∴EG=EF+FG=46(米)
故选:A.


科目:初中数学 来源: 题型:
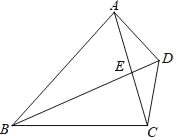
【题目】已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DEDB,求证:
(1)△BCE∽△ADE;
(2)ABBC=BDBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
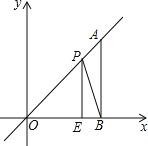
【题目】如图,在平面直角坐标系中,A点为直线y=x上一点,过A点作AB⊥x轴于B点,若OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长的最小值为( )
A.4+2![]() B.4+
B.4+![]() C.6D.4
C.6D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
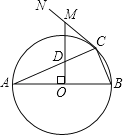
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
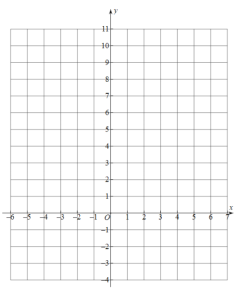
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)判断AG与⊙O的位置关系,并说明理由.
(2)若BA=8,∠B=37°,求直径BC的长(结果精确到0.01).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=![]() ,则tan∠DBC的值是( )
,则tan∠DBC的值是( )
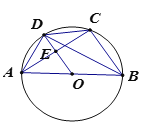
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是___.
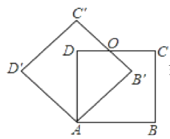
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com