
【题目】综合与探究:
如图,将抛物线![]() 向右平移
向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到的抛物线
个单位长度后,得到的抛物线![]() ,平移后的抛物线
,平移后的抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .抛物线
.抛物线![]() 的对称轴
的对称轴![]() 与抛物线
与抛物线![]() 交于点
交于点![]() .
.

(1)请你直接写出抛物线![]() 的解析式;(写出顶点式即可)
的解析式;(写出顶点式即可)
(2)求出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)可根据二次函数图像左加右减,上加下减的平移规律进行解答.
(2)令x=0即可得到点C的坐标,令y=0即可得到点B,A的坐标
(3)有图像可知![]() 的对称轴,即可得出点D的坐标;由
的对称轴,即可得出点D的坐标;由![]() 图像得出
图像得出![]() 的坐标,设直线
的坐标,设直线![]() 的解析式为
的解析式为![]() ,代入数值,即可得出直线
,代入数值,即可得出直线![]() 的解析式,就可以得出点P的坐标.
的解析式,就可以得出点P的坐标.
解:(1)二次函数![]() 向右平移
向右平移![]() 个单位长度得,
个单位长度得,![]() ,
,
再向下平移![]() 个单位长度得
个单位长度得![]()
故答案为:![]() .
.
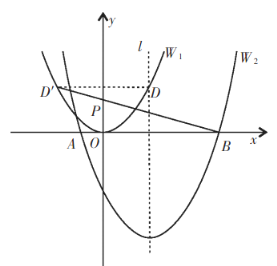
(2)由抛物线![]() 的图象可知,
的图象可知,
![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() .
.
![]() ,
,![]() .
.
(3)由抛物线![]() 的图象可知,
的图象可知,
其对称轴![]() 的为直线
的为直线![]() ,
,
将![]() 代入抛物线
代入抛物线![]() ,可得
,可得
![]() .
.
由抛物线![]() 的图象可知,
的图象可知,
点![]() 关于抛物线
关于抛物线![]() 的对称轴
的对称轴![]() 轴的对称点为
轴的对称点为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
![]()
解得: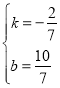
![]() 直线直线
直线直线![]() 的解析式为
的解析式为![]()
与![]() 轴交点即为点
轴交点即为点![]() ,
,
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】中国福利彩票“3D单选”,每期中奖号码是从000,001,002,...,999中随机摇出1个,中奖金额为1000元,每注购买价格2元(只选1个号码,如518),回答下列问题:
(1)若某人买1注,则他中奖是_____事件(用“可能”、“不可能”或“必然”填空),中奖概率是______;
(2)若某人把所有号码各买1注,则他中奖是______事件(用“可能”、“不可能”或“必然”填空),中奖概率是_______,此时他赔_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
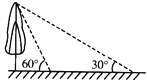
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边行,它是中心对称图形”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
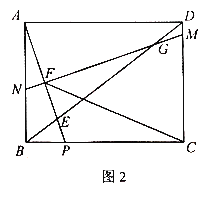
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
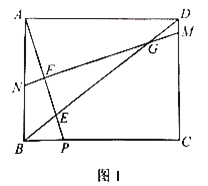
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=![]() ,求sin∠E的值.
,求sin∠E的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的图像与
的图像与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
(1)求该二次函数的表达式及顶点坐标;
(2)画出此二次函数的大致图象;利用图象回答:当![]() 取何值时,
取何值时,![]() ?
?
(3)若点![]() 在抛物线
在抛物线![]() 的图像上,且点
的图像上,且点![]() 到
到![]() 轴距离小于3,则
轴距离小于3,则![]() 的取值范围为 ;
的取值范围为 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,AC=BC,OA=1,OC=4,抛物线y=x2+bx+c经过A,B两点.
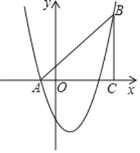
(1)求抛物线的解析式;
(2)点E是直角△ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E、F的坐标;
(3)在(2)的条件下:在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),射线AM∥射线BN,AB是它们的公垂线,点D、C分别在AM、BN上运动(点D与点A不重合、点C与点B不重合),E是AB边上的动点(点E与A、B不重合),在运动过程中始终保持DE⊥EC.
(1)求证:△ADE∽△BEC;
(2)如图(2),当点E为AB边的中点时,求证:AD+BC=CD;
(3)当 AD+DE=AB=![]() 时.设AE=m,请探究:△BEC的周长是否与m值有关?若有关,请用含有m的代数式表示△BEC的周长;若无关,请说明理由.
时.设AE=m,请探究:△BEC的周长是否与m值有关?若有关,请用含有m的代数式表示△BEC的周长;若无关,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com