【题目】如图，菱形ABCD中，对角线AC，BD相交于点O，不添加任何辅助线，要使四边形ABCD是正方形，则需要添加一个条件是 ． （填一个即可） 
轻松暑假总复习系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，△ABC三个顶点的位置如图所示(每个小正方形的边长均为 1)，△ABC中任意一点 P(x，y)平移后的对应点为 P′(x+3，y+2)．
(1)将△ABC按此规律平移后得到△A′B′C′请画出平移后的△A′B′C′(其中 A′，B′，C′分别是A，B，C的对应点，不写画法)．
(2)直接写出 A′，B′，C′三点的坐标：A′(____，____)，B′(____，____)，C′(____，____).
(3)求△A′B′C′的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，已知AB=4，BC=3，矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置，再绕右下角的顶点继续向右旋转90°至图②位置，…，以此类推，这样连续旋转2016次后，顶点A在整个旋转过程中所经过的路程之和是（ ）
A.2015π
B.3019.5π
C.3018π
D.3024π
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时后达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s（km）与小明离家时间t（h）的关系图，请根据图回答下列问题：
（1）图中自变量是____，因变量是______；
（2）小明家到滨海公园的路程为____ km，小明在中心书城逗留的时间为____ h；
（3）小明出发______小时后爸爸驾车出发；
（4）图中A点表示___________________________________；
（5）小明从中心书城到滨海公园的平均速度为______km/h，小明爸爸驾车的平均速度为______km/h；（补充；爸爸驾车经过______追上小明）；
（6）小明从家到中心书城时，他离家路程s与坐车时间t之间的关系式为________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】[数学实验探索活动]
实验材料现有若干块如图①所示的正方形和长方形硬纸片．
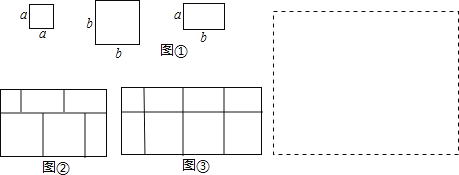
实验目的：
用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径．
例如，选取正方形、长方形硬纸片共 6 块，拼出一个如图②的长方形，计算它的面积， 写出相应的等式有 a2+3ab+2b2=(a+2b)(a+b)或 (a+2b)(a+b) =a2+3ab+2b2．
问题探索：
(1) 小明想用拼图的方法解释多项式乘法(2a+b)(a+b) =2a2+3ab+b2 ，那么需要两种正方形纸片 张，长方形纸片 张；
(2)选取正方形、长方形硬纸片共 8 块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；
(3)试借助拼图的方法，把二次三项式 2a2+5ab+2b2 分解因式，并把所拼的图形画在虚线方框内.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，任意四边形ABCD，对角线AC、BD交于O点，过各顶点分别作对角线AC、BD的平行线，四条平行线围成一个四边形EFGH．试想当四边形ABCD的形状发生改变时，四边形EFGH的形状会有哪些变化？完成以下题目：
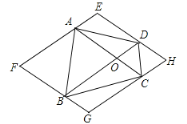
(1)①当ABCD为任意四边形时，四边形EFGH为___________；
②当四边形ABCD为矩形时，四边形EFGH为___________；
③当四边形ABCD为菱形时，四边形EFGH为___________；
④当四边形ABCD为正方形时，四边形EFGH为___________；
(2)请对(1)中①③你所写的结论进行证明
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察一列数：1、2、4、8、16、32、…，发现从第二项开始，每一项与前一项的比值都是同一个常数，这个常数是_______；根据此规律，如果
(
为正整数)表示这个数列的第项，如果
，
，那么
_____，…，
_______；
如果欲求
的值，
可令
…………①
将①式两边同乘以2，得
……………②
由②减去①式，得
.
(2)类比可得：
__________.
(3)用由特殊到一般的方法知：若数列
、
、
、…、，从第二项开始每一项与前一项之比的常数为
，那么
，____，…，______ (用含，
，的代数式表示).
用含，，的代数式表示
_________.
(4)一质点从距离原点一个单位的A点向原点方向跳动，第一次跳到OA中点
处，第二次从跳到
的中点
处，第三次从跳到
的中点
处，…，如此不断跳下去，则第50次跳动后，该质点跳动的距离是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：点A在射线CE上，∠C＝∠D．
⑴如图1，若AD∥BC，求证：BD∥AC；
⑵如图2，若∠BAC＝∠BAD，BD⊥BC，请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；
⑶如图3，在⑵的条件下，过点D作DF∥BC交射线于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
