
已知抛物线 上有不同的两点E
上有不同的两点E 和F
和F .
.
(1)求抛物线的解析式.
(2)如图,抛物线 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)当m,n为何值时,∠PMQ的边过点F.
(1)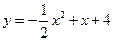
(2)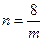 (m>0)
(m>0)
(3)当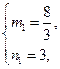
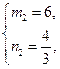
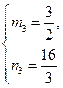 或
或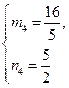 时,∠PMQ的边过点F
时,∠PMQ的边过点F
解析解:(1)抛物线 的对称轴为
的对称轴为 . ……..(1分)
. ……..(1分)
∵ 抛物线上不同两个点E 和F
和F 的纵坐标相同,
的纵坐标相同,
∴ 点E和点F关于抛物线对称轴对称,则 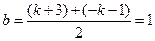 ,且k≠-2.
,且k≠-2.
∴ 抛物线的解析式为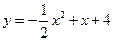 . ……..(2分)
. ……..(2分)
(2)抛物线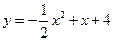 与x轴的交点为A(4,0),与y轴的交点为B(0,4),
与x轴的交点为A(4,0),与y轴的交点为B(0,4),
∴ AB=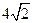 ,AM=BM=
,AM=BM= . ……..(3分)
. ……..(3分)
在∠PMQ绕点M在AB同侧旋转过程中,∠MBC=∠DAM=∠PMQ=45°,
在△BCM中,∠BMC+∠BCM+∠MBC=180°,即∠BMC+∠BCM=135°,
在直线AB上,∠BMC+∠PMQ+∠AMD=180°,即∠BMC+∠AMD=135°.
∴ ∠BCM=∠AMD.
故 △BCM∽△AMD. ……..(4分)
∴ 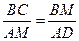 ,即
,即 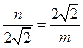 ,
,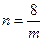 .
.
故n和m之间的函数关系式为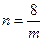 (m>0). ……..(5分)
(m>0). ……..(5分)
(3)∵ F 在
在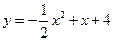 上,
上,
∴  ,
,
化简得,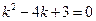 ,∴ k1=1,k2=3.
,∴ k1=1,k2=3.
即F1(-2,0)或F2(-4,-8). ……..(6分)
①MF过M(2,2)和F1(-2,0),设MF为 ,
,
则 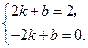 解得,
解得, ∴ 直线MF的解析式为
∴ 直线MF的解析式为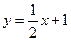 .
.
直线MF与x轴交点为(-2,0),与y轴交点为(0,1).
若MP过点F(-2,0),则n=4-1=3,m=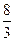 ;
;
若MQ过点F(-2,0),则m=4-(-2)=6,n=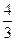 . ……..(7分)
. ……..(7分)
②MF过M(2,2)和F1(-4,-8),设MF为 ,
,
则  解得,
解得,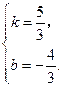 ∴ 直线MF的解析式为
∴ 直线MF的解析式为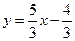 .
.
直线MF与x轴交点为(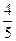 ,0),与y轴交点为(0,
,0),与y轴交点为(0,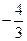 ).
).
若MP过点F(-4,-8),则n=4-(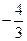 )=
)=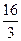 ,m=
,m=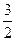 ;
;
若MQ过点F(-4,-8),则m=4-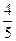 =
= ,n=
,n=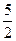 . ……..(8分)
. ……..(8分)
故当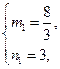
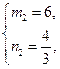
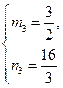 或
或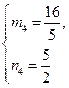 时,∠PMQ的边过点F.
时,∠PMQ的边过点F.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
已知抛物线![]() 上有不同的两点E
上有不同的两点E![]() 和F
和F![]() .
.
(1)求此抛物线的解析式.
(2)如图,抛物线![]() 与x轴的正半轴和y轴分别交于点A和点B,M为AB的中点,∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.∠PMQ在AB的左侧以M为中心旋转,设AD 的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
与x轴的正半轴和y轴分别交于点A和点B,M为AB的中点,∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.∠PMQ在AB的左侧以M为中心旋转,设AD 的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)在(2)的条件下,当m,n为何值时,∠PMQ的边过点F.
 |
查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》中考题集(30):6.4 二次函数的应用(解析版) 题型:解答题
 上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1).
上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1). 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源:第26章《圆》中考题集(06):26.1 旋转(解析版) 题型:解答题
 上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1).
上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1). 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;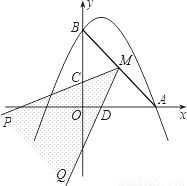
查看答案和解析>>
科目:初中数学 来源:2010年全国中考数学试题汇编《二次函数》(08)(解析版) 题型:解答题
 上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1).
上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1). 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
查看答案和解析>>
科目:初中数学 来源:2010年四川省南充市中考数学试卷(解析版) 题型:解答题
 上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1).
上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1). 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com