
【题目】为弘扬遵义红色文化,传承红色文化精神,某校准备组织学生开展研学活动.经了解,有A.遵义会议会址、B.苟坝会议会址、C.娄山关红军战斗遗址、D.四渡赤水纪念馆共四个可选择的研学基地.现随机抽取部分学生对基地的选择进行调查,每人必须且只能选择一个基地.根据调查结果绘制如下不完整的条形统计图和扇形统计图.
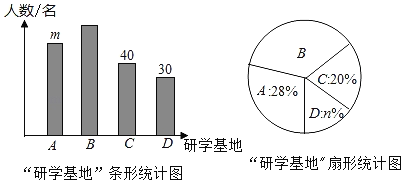
(1)统计图中m= ,n= ;
(2)若该校有1500名学生,请估计选择B基地的学生人数;
(3)某班在选择B基地的4名学生中有2名男同学和2名女同学,需从中随机选出2名同学担任“小导游”,请用树状图或列举法求这2名同学恰好是一男一女的概率.
【答案】(1)56,15;(2)555人;(3)![]() .
.
【解析】
(1)先由C类别人数及其所占百分比求出总人数,再进一步求解可得;
(2)用总人数乘以样本中选择B基地的学生人数所占比例即可得;
(3)根据题意画出树状图得出所有等情况数,找出选出的2名学生恰好是一男一女的情况数,然后根据概率公式即可得出答案.
解:(1)由题意可知:总人数为40÷20%=200(人)
所以m=200×28%=56(人),n%=![]() ×100%=15%,即n=15,
×100%=15%,即n=15,
故答案为:56,15;
(2)估计选择B基地的学生人数1500×![]() =555(人);
=555(人);
(3)根据题意画出树状图如下:
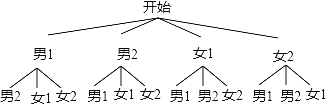
一共有12种情况,恰好是1男1女的情况有8种,
∴这2名同学恰好是一男一女的概率为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,某社区工作人员在社区随机抽取了若干名居民开展环保知识有奖问答活动,并用得到的数据绘制了如图所示条形统计图(得分为整数,满分为10分,最低分为6分).
请根据图中信息,解答下列问题:
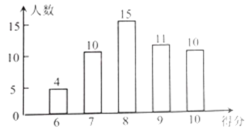
(1)本次调查一共抽取了__________名居民;
(2)求本次调查获取的样本数据的平均数;并直接写出样本数据的众数和中位数;
(3)社区决定对该小区500名居民开展这项有奖问答活动,得10分者设为“一等奖”.根据调查结果,请你帮社区工作人员直接估计出需准备多少份“一等奖”奖品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快“智慧校园”建设,某县准备为试点学校采购一批 ![]() 、
、![]() 两种型号的一体机.经过市场调查发现,今年每套
两种型号的一体机.经过市场调查发现,今年每套 ![]() 型一体机的价格比每套
型一体机的价格比每套 ![]() 型一体机的价格多
型一体机的价格多 ![]() 万元,且用
万元,且用![]() 万元恰好能购买
万元恰好能购买 ![]() 套
套 ![]() 型一体机和
型一体机和 ![]() 套
套 ![]() 型一体机.
型一体机.
(1)求今年每套 ![]() 型、
型、![]() 型一体机的价格各是多少万元?
型一体机的价格各是多少万元?
(2)该县明年计划采购 ![]() 型、
型、![]() 型一体机共
型一体机共 ![]() 套,需投入资金
套,需投入资金 ![]() 万元. 考虑物价因素,预计明年每套
万元. 考虑物价因素,预计明年每套 ![]() 型一体机的价格不变,每套
型一体机的价格不变,每套 ![]() 型一体机的价格比今年上涨
型一体机的价格比今年上涨 ![]() , 设该市明年购买
, 设该市明年购买 ![]() 型一体机
型一体机 ![]() 套.
套.
①请写出该县明年需投入资金 ![]() (万元)与购买
(万元)与购买 ![]() 型一体机
型一体机 ![]() (套)之间的函数关系式 ;
(套)之间的函数关系式 ;
②若该县明年购买 ![]() 型一体机的总费用不低于购买
型一体机的总费用不低于购买 ![]() 型一体机的总费用,那么该县明年至少需要投入多少万元才能完成采购计划?
型一体机的总费用,那么该县明年至少需要投入多少万元才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 将一列有理数﹣1,2,﹣3,4,﹣5,6…如图所示有序排列,4所在位置为峰1,﹣9所在位置为峰2….
(1)处在峰5位置的有理数是_____;
(2)2022应排在A,B,C,D,E中_____的位置上.
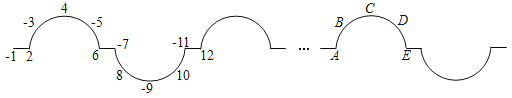
查看答案和解析>>
科目:初中数学 来源: 题型:
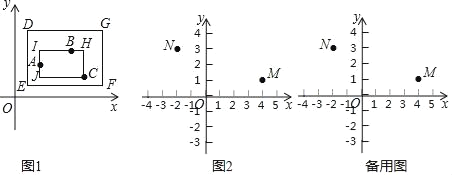
【题目】平面直角坐标系xOy中,对于任意的三个点A、B、C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的“三点矩形”.在点A,B,C的所有“三点矩形”中,若存在面积最小的矩形,则称该矩形为点A,B,C的“最佳三点矩形”.
如图1,矩形DEFG,矩形IJCH都是点A,B,C的“三点矩形”,矩形IJCH是点A,B,C的“最佳三点矩形”.
如图2,已知M(4,1),N(﹣2,3),点P(m,n).
(1)①若m=1,n=4,则点M,N,P的“最佳三点矩形”的周长为 ,面积为 ;
②若m=1,点M,N,P的“最佳三点矩形”的面积为24,求n的值;
(2)若点P在直线y=﹣2x+4上.
①求点M,N,P的“最佳三点矩形”面积的最小值及此时m的取值范围;
②当点M,N,P的“最佳三点矩形”为正方形时,求点P的坐标;
(3)若点P(m,n)在抛物线y=ax2+bx+c上,且当点M,N,P的“最佳三点矩形”面积为12时,﹣2≤m≤﹣1或1≤m≤3,直接写出抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
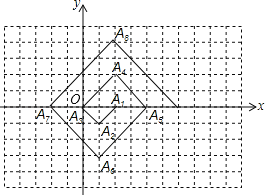
【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
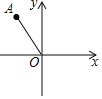
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,![]() ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
A.(0,﹣2)B.(1,﹣![]() )C.(2,0)D.(
)C.(2,0)D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
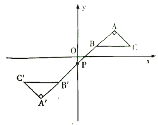
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
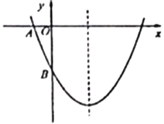
【题目】如图,已知二次函数![]() 的图像与坐标轴交于点
的图像与坐标轴交于点![]() 和点
和点![]() .
.
(1)求该二次函数的解析式;
(2)已知该函数图像的对称轴上存在一点![]() ,使得
,使得![]() 的周长最小.请求出点
的周长最小.请求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 是等腰三角形,请直接写出所有符合条件的点
是等腰三角形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com