
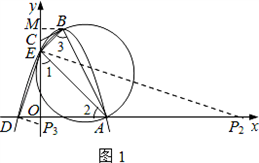
 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
 =3
=3 .
.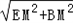 =
= .
. =
= =tan∠CBE,
=tan∠CBE, ,sin∠BAE=
,sin∠BAE=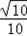 ,cos∠BAE=
,cos∠BAE=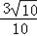 ;
; =tan∠BAE,即∠DEO=∠BAE满足△DEO∽△BAE的条件,
=tan∠BAE,即∠DEO=∠BAE满足△DEO∽△BAE的条件,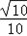 ;
;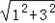 =
=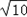 ,则DP2=DE×sin∠DP2E=
,则DP2=DE×sin∠DP2E=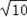 ×
× =10,OP2=DP2﹣OD=9
=10,OP2=DP2﹣OD=9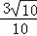 ;
;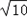 ×
×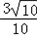 =
= ,OP3=EP3﹣OE=
,OP3=EP3﹣OE= ;
; ).
).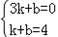 解得
解得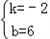
 ,∴F(
,∴F( ,3).
,3). 时,
时,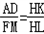 ,即
,即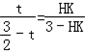 .
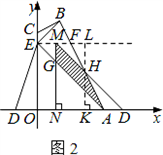
. ×3×3﹣
×3×3﹣ (3﹣t)2﹣
(3﹣t)2﹣ t×2t=﹣
t×2t=﹣ t2+3t.
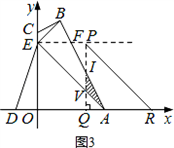
t2+3t. <t≦3时,
<t≦3时,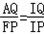 .
.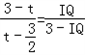 ,解得IQ=2(3﹣t).
,解得IQ=2(3﹣t). ×(3﹣t)×2(3﹣t)﹣
×(3﹣t)×2(3﹣t)﹣ (3﹣t)×2=
(3﹣t)×2= (3﹣t)2=
(3﹣t)2= t2﹣3t+
t2﹣3t+ .
. .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
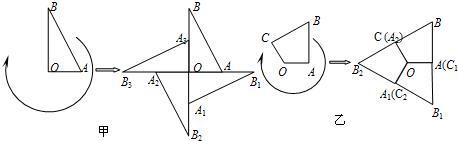
查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》中考题集(08):25.2 旋转变换(解析版) 题型:选择题
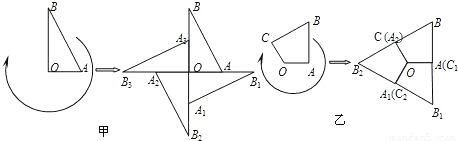

查看答案和解析>>
科目:初中数学 来源:第26章《圆》中考题集(02):26.1 旋转(解析版) 题型:选择题
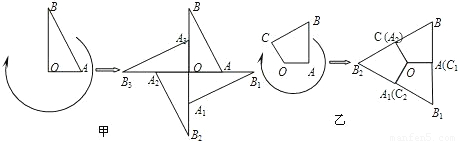

查看答案和解析>>
科目:初中数学 来源:第23章《旋转》中考题集(02):23.1 图形的旋转(解析版) 题型:选择题
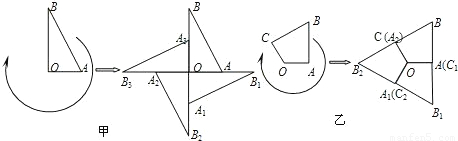

查看答案和解析>>
科目:初中数学 来源:2009-2010学年九年级数学上册期中综合水平测试卷A卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com