
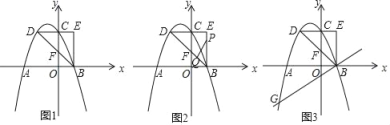
����Ŀ�� ��ͼ1����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y��ax2+bx+5��x�ύ��A����B����y�ύ�ڵ�C������C��CD��y�ύ�������ڵ�D������B��BE��x�ᣬ��DC�ӳ����ڵ�E������BD����y���ڵ�F��ֱ��BD�Ľ���ʽΪy����x+2��
��1��д����E�����ꣻ�����ߵĽ���ʽ��
��2����ͼ2����P���߶�EB�ϴӵ�E���B��1����λ����/����ٶ��˶���ͬʱ����Q���߶�BD�ϴӵ�B���D��![]() ����λ����/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PQBΪֱ�������Σ�
����λ����/����ٶ��˶�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶�����tΪ��ֵʱ����PQBΪֱ�������Σ�
��3����ͼ3������B��ֱ��BG���������ڵ�G����tan��ABG��![]() ����MΪֱ��BG�Ϸ���������һ�㣬����M��MH��BG������ΪH����HF��MF����ֱ��д�����������ĵ�M�����꣮
����MΪֱ��BG�Ϸ���������һ�㣬����M��MH��BG������ΪH����HF��MF����ֱ��д�����������ĵ�M�����꣮
���𰸡���1����E����Ϊ��2��5����y����![]() x2��
x2��![]() +5����2��t��
+5����2��t��![]() ��
��![]() ʱ����PQBΪֱ�������Σ���3����M����Ϊ����4��3����0��5����
ʱ����PQBΪֱ�������Σ���3����M����Ϊ����4��3����0��5����
��������
��1���ɴ���ϵ����������꼰������ϵʽ��
��2���������⣬��DEBΪ����ֱ�������Σ�ͨ���������ۡ�PQB=90�����QPB=90������������������tֵ��
��3���ӳ�MF��GB��K���ɡ�MHK=90����HF=MF���Ƶ�HF=FK����FΪMK�е㣬���M���꣬�����е��������ʣ���ʾK�����꣬����GB����ʽ������õ�M���꣮
����D��-3��5����B��2��0������y=ax2+bx+5
![]()
���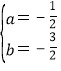
�������߽���ʽΪ��y=-![]() x2-
x2-![]() x+5
x+5
��2������֪��QBE=45����PE=t��PB=5-t��QB=![]() t
t
����QPB=90��ʱ����PQBΪֱ�������Σ�
�ߡ�QBE=45��
��QB=![]() PB
PB
��![]() t��
t��![]() (5t)
(5t)
���t=![]()
����PQB=90��ʱ����PQBΪֱ�������Σ�
��BPQ�ס�BDE
��BQBD=BPBE
��5��5-t��=![]() t5
t5![]()
��ã�t=![]()
��t=![]() ��
��![]() ʱ����PQBΪֱ�������Σ�
ʱ����PQBΪֱ�������Σ�
��3������֪tan��ABG=![]() ����ֱ��GB��B��
����ֱ��GB��B��
��ֱ��GB����ʽΪ��y=![]() x1
x1
�ӳ�MF��ֱ��BG�ڵ�K
��HF=MF
���FMH=��FHM
��MH��BGʱ
���FMH+��MKH=90��
��FHK+��FHM=90��
���FKH=��FHK
��HF=KF
��FΪMK�е�
���M������x��-![]() x2-
x2-![]() x+5��
x+5��
��F��0��2��
���K������-x��![]() x2+
x2+![]() x-1��
x-1��
��K���������y=![]() x1
x1
���x1=0��x2=-4��
��x=0����y=-![]() x2-
x2-![]() x+5�����y=5��
x+5�����y=5��
��x=-4����y=-![]() x2-
x2-![]() x+5
x+5
���y=3
���M������-4��3����0��5����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ���
���![]() ����
����![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ������
������![]() .
.
��1����ͼ������![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��������߶�
��������߶�![]() �ij���
�ij���
��2����ͼ����![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() �ϵĶ��㣨�����
�ϵĶ��㣨�����![]() �غϣ�����
�غϣ�����![]() �ܳ�����Сֵ.
�ܳ�����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ���������ύ�ڵ�A��1�� 0���͵�C��������A��ֱ��
��ͼ���������ύ�ڵ�A��1�� 0���͵�C��������A��ֱ��![]() ����κ���ͼ������һ��B����B���C���ڶ��κ���ͼ��ĶԳ���Գƣ�
����κ���ͼ������һ��B����B���C���ڶ��κ���ͼ��ĶԳ���Գƣ�
��1����һ�κ�������ʽ��
��2����P�ڶ��κ���ͼ��ĶԳ����ϣ�����ACP���ܳ���Сʱ���������P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ij���۹��������ص�EΪ�ļ���Ŀ��������.��֪��E������������AB�ľ���OEΪ10��,����ABΪ123��(AB��ֱ����BC),�ڵ���C����õ�E�����Ǧ�=45��,�ӵ�C��CB����ǰ��40����D��,��D���������A�����Ǧ�=60��,���E�����ĸ߶�EF.(�����ȷ��0.1��)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Oֱ����C��DΪ��O�ϵĵ㣬��ACD��2��A��CE��DB��DB���ӳ����ڵ�E��
��1����֤��ֱ��CE���O���У�
��2����AC��8��AB��10����CE�ij���
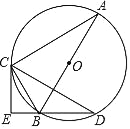
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ǰ���![]() ����(
����(![]() )�ĸ������ȷ֣��ֱ��Ծ��е������߶�Ϊһ����������
)�ĸ������ȷ֣��ֱ��Ծ��е������߶�Ϊһ����������![]() ���Σ���ȥ�����е������߶Σ��õ�һ���µ�ͼ�ν�����
���Σ���ȥ�����е������߶Σ��õ�һ���µ�ͼ�ν�����![]() ���ε�����չͼ�������������ı�����Ϊ
���ε�����չͼ�������������ı�����Ϊ![]() ����ͼ
����ͼ![]() �����������ν�������������õ�������չͼ��������
�����������ν�������������õ�������չͼ��������![]() .ͼ
.ͼ![]() ��ͼ
��ͼ![]() �ֱ���������Ρ��������ε�����չͼ������
�ֱ���������Ρ��������ε�����չͼ������
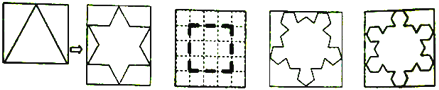
(1)��ͼ![]() ����
����![]() ���������������ýϴֵ�������һ�������Σ�����ͼ
���������������ýϴֵ�������һ�������Σ�����ͼ![]() ����ʵ�����������ε�����չͼ������
����ʵ�����������ε�����չͼ������
(2)��֪![]() ����ͼ
����ͼ![]() ��
��![]() =_____���������Ϲ��ɣ���
=_____���������Ϲ��ɣ���![]() ���ε�����չͼ������
���ε�����չͼ������![]() =______��(�ú�
=______��(�ú�![]() ��ʽ�ӱ�ʾ)
��ʽ�ӱ�ʾ)
(3)��֪![]() ����
����![]() ����
����![]() =_____.
=_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У���DAB=60�㣬AB=AD���߶�BC�Ƶ�B˳ʱ����ת60���õ��߶�BE������AC��ED��
��1����֤��AC=DE��
��2����DC=4��BC=6����DCB=30������AC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ѱ뾶Ϊ![]() ��
��![]() ����
����![]() �۵���
�۵���![]() ����Բ��
����Բ��![]() ������Ӱ���ֵ����Ϊ__________�����������
������Ӱ���ֵ����Ϊ__________�����������![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�ѧ��ÿ�ܽ�������������ʱ���������ȫ��![]() ��ѧ�����е��飬��ÿ�ܽ�������������ʱ��
��ѧ�����е��飬��ÿ�ܽ�������������ʱ��![]() ����λ��Сʱ������ѧ���ֳ����ࣺ
����λ��Сʱ������ѧ���ֳ����ࣺ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .���Ƴ��в�����������ͳ��ͼ��ͼ. ����������Ϣ������������⣺
.���Ƴ��в�����������ͳ��ͼ��ͼ. ����������Ϣ������������⣺
��1��![]() ��ѧ���� �ˣ���ȫ����ͳ��ͼ��
��ѧ���� �ˣ���ȫ����ͳ��ͼ��
��2��![]() ��ѧ������ռ�������������� %��
��ѧ������ռ�������������� %��
��3���Ӹð�ÿ�ܽ�����������ʱ����![]() ��ѧ������ѡ��
��ѧ������ѡ��![]() �ˣ�����
�ˣ�����![]() ��ÿ�ܽ�����������ʱ�䶼��
��ÿ�ܽ�����������ʱ�䶼��![]() �еĸ���.
�еĸ���.
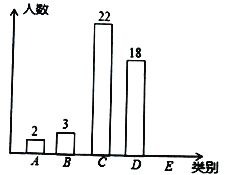
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com