
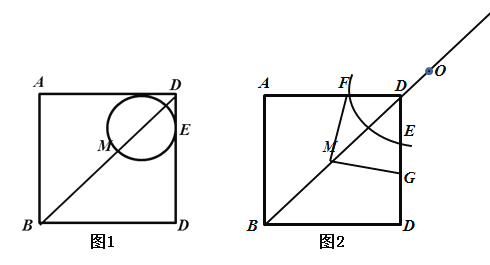
【题目】已知正方形ABCD的边长为2,中心为M,⊙O的半径为r,圆心O在射线BD上运动,⊙O与边CD仅有一个公共点E.
(1)如图1,若圆心O在线段MD上,点M在⊙O上,OM=DE,判断直线AD与⊙O的位置关系,并说明理由;
(2)如图2,⊙O与边AD交于点F,连接MF,过点M作MF的垂线与边CD交于点G,若![]() ,设点O与点M之间的距离为
,设点O与点M之间的距离为![]() ,EG=
,EG=![]() ,当
,当![]() 时,求
时,求![]() 的函数解析式.
的函数解析式.
【答案】(1)相切,证明详见解析;(2) .
.
【解析】
(1)过O作OF⊥AD于F,连接OE,可证△ODF≌△ODE,可得OF=OE,根据相切判定即可得出:AD与![]() 相切;
相切;
(2)连接MC,可证![]() ,可得DF=CG,过点E作EP⊥BD于P,过点F作FH⊥BD于H设DP=a,DH=b,由于△DHF与△DPE都是等腰直角三角形,设EP=DP=a,FH=DH=b,利用勾股定理:可列出方程组
,可得DF=CG,过点E作EP⊥BD于P,过点F作FH⊥BD于H设DP=a,DH=b,由于△DHF与△DPE都是等腰直角三角形,设EP=DP=a,FH=DH=b,利用勾股定理:可列出方程组 解得a=b,可得
解得a=b,可得![]() ,
, ![]() .由于
.由于![]() 可得
可得![]() ,由
,由![]() 可得OD=a, 由OD=OM-DM,可得
可得OD=a, 由OD=OM-DM,可得![]() , 代入2DF+y=2可得
, 代入2DF+y=2可得![]() ,整理得y与x的函数解析式,由DF≤1, EG≥0,可得x的取值范围,即可求解问题.
,整理得y与x的函数解析式,由DF≤1, EG≥0,可得x的取值范围,即可求解问题.
解:(1)直线AD与⊙O相切,理由如下:
过O作OF⊥AD于F,连接OE

∴∠OFD=90°
在正方形ABCD中,BD平分∠ADE,∠ADE=90°
∴∠FDO=∠EDO=45°
∵![]() 与CD仅有一个公共点E
与CD仅有一个公共点E
∴CD与![]() 相切
相切
∴OE⊥DC,OE为![]() 半径
半径
∴∠OED=90°
又∵OD=OD
∴△ODF≌△ODE
∴OF=OE
∵OF⊥AD、OF=OE
∴AD与![]() 相切
相切
(2)连接MC

在正方形ABCD中,∠BCD=90°,∠ADB =45°
∵∠BCD=90°,M为正方形的中心
∴MC=MD=![]() ,∠ADB=∠DCM=45°
,∠ADB=∠DCM=45°
∵FM⊥MG,即∠FMG=90°
且在正方形ABCD中,∠DMC=90°
∴∠FMD+∠DMG=∠DMG+∠CMG
∴∠FMD=∠CMG
∴![]()
∴DF=CG
过点E作EP⊥BD于P,过点F作FH⊥BD于H
设DP=a,DH=b
∵∠FDM=∠EDM=45°
∴△DHF与△DPE都是等腰直角三角形
∴EP=DP=a,FH=DH=b
∵![]() ,且由(1)得
,且由(1)得![]()
∴点O在正方形ABCD外
∴OP=OD+DP,OH=OD+DH
在Rt△OPE与Rt△OHF中

![]() 得:(a-b)(OD+a+b)=0
得:(a-b)(OD+a+b)=0
∴a-b=0或OD+a+b=0
∵OD+a+b>0
∴a-b=0
∴a=b
即点P与点H重合,也即EF⊥BD,垂足为P(或H)
∵DP=a,DH=b
∵在Rt△DPE中,![]()
在Rt△DHF中,![]()
∴DF=DE
∵CD=DE+EG+CG=2,即2DF+EG=2
∴2DF+y=2
∵在Rt△DPF中,![]() ,且
,且![]()
∴![]()
在Rt△OPE与Rt△OHF中
![]()
∴![]()
∴OD+a=2a
∴OD=a
又因为 OD=OM-DM,即![]()
∴![]()
又因为 2DF+y=2
∴![]()
∴![]()
∴![]()
∵DF≤1,且2DF+EG=2
∴EG≥0,即y≥0
∴
∴![]()
∴y与x的函数解析式为


科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.

(1)求∠PCQ的度数;
(2)当AB=4,AP=![]() 时,求PQ的大小;
时,求PQ的大小;
(3)当点P在线段AC上运动时(P不与A,C重合),求证:2PB2=PA2+PC2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日6时至10时,某交易平台上一种水果的每千克售价、每千克成本与交易时间之间的关系分别如图1、图2所示(图1、图2中的图象分别是线段和抛物线,其中点P是抛物线的顶点).在这段时间内,出售每千克这种水果收益最大的时刻是_____ ,此时每千克的收益是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售一种进价为10元1件的饰品,经调查发现,该饰品的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)满足函数
(元)满足函数![]() ,设销售这种饰品每天的利润为
,设销售这种饰品每天的利润为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当销售单价定为多少元时,该商城获利最大?最大利润为多少?
(3)在确保顾客得到优惠的前提下,该商城还要通过销售这种饰品每天获利750元,该商城应将销售单价定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区检票口有A、B、C、D共4个检票通道.甲、乙两人到该景区游玩,两人分别从4个检票通道中随机选择一个检票.
(1)甲选择A检票通道的概率是 ;
(2)求甲乙两人选择的检票通道恰好相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,给出如下定义:若点
中,给出如下定义:若点![]() 在图形
在图形![]() 上,点
上,点![]() 在图形
在图形![]() 上,如果
上,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 的“近距离”,记为
的“近距离”,记为![]() .特别地,当图形
.特别地,当图形![]() 与图形
与图形![]() 有公共点时,
有公共点时,![]() .
.
已知![]() ,
,![]() ,
,![]() ,
,
(1)![]() 点
点![]() ,点
,点![]()
![]() ,
,![]() 点
点![]() ,线段
,线段![]()
![]() ;
;
(2)⊙![]() 半径为
半径为![]() ,
,
①当![]() 时,求⊙
时,求⊙![]() 与线段
与线段![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,线段
,线段![]() ;
;
②若![]() ⊙
⊙![]() ,
,![]()
![]() ,则
,则![]() .
.
(3)![]() 为
为![]() 轴上一点,⊙
轴上一点,⊙![]() 的半径为1,点
的半径为1,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,⊙
,⊙![]() 与
与![]() 的“近距离”
的“近距离”![]() ⊙
⊙![]() ,
,![]() ,请直接写出圆心
,请直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
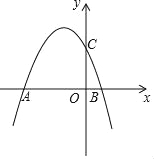
【题目】如图,二次函数y=ax2﹣![]() x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
x+2(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,已知点A(﹣4,0).
(1)求抛物线与直线AC的函数解析式;
(2)若点D(m,n)是抛物线在第二象限的部分上的一动点,四边形OCDA的面积为S,求S关于m的函数关系;
(3)若点E为抛物线上任意一点,点F为x轴上任意一点,当以A、C、E、F为顶点的四边形是平行四边形时,请直接写出满足条件的所有点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com