
如图,已知AB∥CD,∠AEC=90°,那么∠A与∠C的度数和为多少度?为什么?
【解析】
∠A与∠C的度数和为 _________ .
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°( _________ ).
∵AB∥CD( _________ ),EF∥AB,
∴EF∥CD( _________ )
∴ _________ (两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= _________ °(等式的性质)
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°(已知)
∴∠A+∠C= _________ °(等式的性质).

270°,完成理由证明见解析.
【解析】
试题分析:
关键是过点E作EF∥AB,
则利用两直线平行,同旁内角互补。得∠A+∠AEF=180°
再有AB∥CD和 EF∥AB,可知EF∥CD
由两直线平行,同旁内角互补,得到∠C+∠CEF=180°
则得到∠A+∠AEF+∠CEF+∠C=360°,据等式的性质 即∠A+∠AEC+∠C=360°
又∠AEC=90°得到∠A+∠C=270°.
试题解析:∠A与∠C的度数和为 270°.
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°(两直线平行,同旁内角互补).
∵AB∥CD( 已知 ),EF∥AB,
∴EF∥CD(平行于同一条直线的两条直线互相平行)
∴∠C+∠CEF=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= 360°(等式的性质)
即∠A+∠AEC+∠C= 360°°
∵∠AEC=90°(已知)
∴∠A+∠C= 270°(等式的性质).
考点:两直线平行,同旁内角互补.


科目:初中数学 来源:2016届浙江省台州市七年级下学期期中考试数学试卷(解析版) 题型:解答题
补全下列各题解题过程.(6分)
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证DF∥AC.
证明:∵∠1=∠2(已知)
∠2=∠3 ∠1=∠4 ( )
∴∠3=∠4 ( 等量代换 )
∴_DB__∥_____ ( )
∴∠C=∠ABD ( )
∵∠C=∠D ( 已 知 )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
科目:初中数学 来源:2016届河北省邢台市沙河市七年级下学期期末数学试卷(解析版) 题型:选择题
下列各因式分解正确的是( )
A.x2+2x-1=(x-1)2 B.-x2+(-2)2=(x-2)(x+2)
C.x3-4x=x(x+2)(x-2) D.(x+1)2=x2+2x+1
查看答案和解析>>
科目:初中数学 来源:2016届河北省邢台市沙河市七年级下学期期末数学试卷(解析版) 题型:选择题
下列长度的各组线段能组成一个直角三角形的是( )
A.4cm,6cm,11cm B.4cm,5cm,1cm
C.3cm,4cm,5cm D.2cm,3cm,6cm
查看答案和解析>>
科目:初中数学 来源:2016届河北省滦南县七年级下学期期中考试数学试卷(解析版) 题型:填空题
如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF= 度.
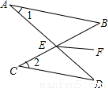
查看答案和解析>>
科目:初中数学 来源:2016届江西省抚州市黎川县七年级下学期期末数学试卷(解析版) 题型:解答题
已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC

证明:∵EF⊥AB CD⊥AB
∴∠EFA=∠CDA=90°(垂直定义)
∠1=∠
∴EF∥CD
∴∠1=∠2(已知)
∴∠2=∠ACD(等量代换)
∴DG∥AC
∴∠DGB=∠ACB
∵AC⊥BC(已知)
∴∠ACB=90°(垂直定义)
∴∠DGB=90°即DG⊥BC.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省七年级下学期期中联考数学试卷(解析版) 题型:解答题
已知:△ABC中,AE平分∠BAC。
(1)如图①AD⊥BC于D,若∠C =70°,∠B =30°,则∠DAE= ;
(2)如图②所示,在△ABC中AD⊥BC,AE平分∠BAC,F是AE上的任意一点,过F作FG⊥BC于G,且∠B=40°,∠C=80°,求∠EFG的度数;
(3)在(2)的条件下,若F点在AE的延长线上(如图③),其他条件不变,则∠EFG的角度大小发生改变吗?说明理由.
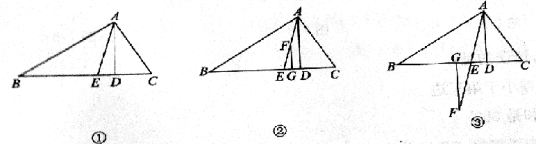
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com