
【题目】如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)

解:∵EF∥AD,(已知)
∴∠2= ( )
∵∠1=∠2,(已知)
∴∠1= ( )
∴ ∥ ,( )
∴∠AGD+ =180°,(两直线平行,同旁内角互补)
∵∠BAC=70°,(已知)
∴∠AGD= (等式性质)
【答案】∠3;两直线平行同位角相等;∠3;等量代换;DG;BA;内错角相等两直线平行;∠CAB;110°.
【解析】
由EF与AD平行,利用两直线平行同位角相等得到∠2=∠3,再由∠1=∠2,利用等量代换得到一对内错角相等,利用内错角相等两直线平行得到DG与BA平行,利用两直线平行同旁内角互补即可求出∠AGD度数.
解:∵EF∥AD,(已知)
∴∠2=∠3(两直线平行同位角相等)
∵∠1=∠2,(已知)
∴∠1=∠3(等量代换)
∴DG∥BA,(内错角相等两直线平行)
∴∠AGD+∠CAB=180°,(两直线平行,同旁内角互补)
∵∠CAB=70°,(已知)
∴∠AGD=110°(等式性质).
故答案为:∠3;两直线平行同位角相等;∠3;等量代换;DG;BA;内错角相等两直线平行;∠CAB;110°.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
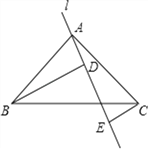
【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
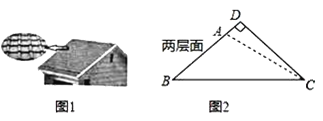
【题目】太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A,B分别在x,y轴上,点C是OB的中点,BE,CD都与x轴平行,BD⊥AB,∠ABO=30°.
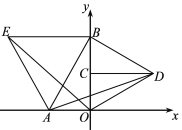
(1)判断△OBD的形状;
(2)若A(-3,0),BE=6,求证OE=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
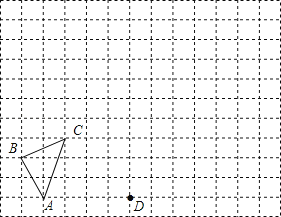
【题目】如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(﹣3,0)、(﹣2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1;
(3)以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() 的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
的图象如图所示,则以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(-1,a),点B(2,b)在图象上,则a <b;④若点P(x,y)在图象上,则点P1(-x,y)也在图象上.其中正确的个数为( )
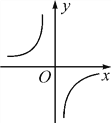
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
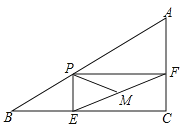
【题目】在Rt△ABC中,∠C=90°,AB=5,AC=3,点P为边AB上一动点(且点P不与点A,B重合),PE⊥BC于E,PF⊥AC于F,点M为EF中点,则PM的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com