
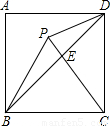
 ×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD=
×2×2sin 30°=1,S△BPD=S△BPC+S△CPD-S△BCD= ×2×2sin60°+1-2×2×
×2×2sin60°+1-2×2× =
=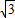 +1-2=
+1-2=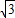 -1.
-1.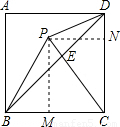 解:过P作PM⊥BC于M,PN⊥CD于N,
解:过P作PM⊥BC于M,PN⊥CD于N,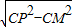 =
=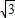 ,
, CD×PN=
CD×PN= ×2×1=1
×2×1=1 ×2×
×2×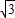 +1-2×2×
+1-2×2× =
=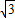 +1-2=
+1-2= -1.
-1.

 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:2006年浙江省杭州市中考数学试卷(课标卷)(解析版) 题型:选择题
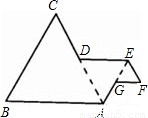
查看答案和解析>>
科目:初中数学 来源:2006年浙江省杭州市中考数学试卷(大纲卷)(解析版) 题型:解答题
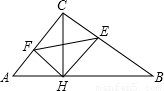
查看答案和解析>>
科目:初中数学 来源:2006年浙江省杭州市中考数学试卷(大纲卷)(解析版) 题型:选择题
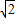 ,则此三角形移动的距离PP′是( )
,则此三角形移动的距离PP′是( )

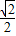
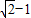
查看答案和解析>>
科目:初中数学 来源:2006年浙江省杭州市中考数学试卷(大纲卷)(解析版) 题型:选择题
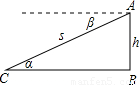
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com