
����Ŀ��Ϊ�˽��οͶ�ij����������ȣ��ض��οͲ�ȡ��������ķ�ʽ�����ʾ����飬����Ľ����ΪA��B��C��D���࣬�京�����α�ʾΪ���dz������������Ƚ���������������������������̫����������������������������1������������
��1����������a��b��
��2��������ݱ���Ƶ��������ͳ��ͼ����ô���ΪB��Ƶ������Ӧ������Բ�Ľ��Ǽ��ȣ�
��3����֪�þ���ÿ���ο�����3000��������һ����ο������C���ο�������
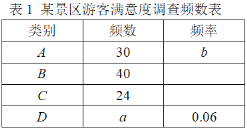
���𰸡���1��a=6��b=0.3����2��144�㣻��3��720��
��������
��1������D��Ƶ����Ƶ���з������![]() ������
������![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��2�������ΪB���ο�����ռ�İٷֱȳ���360�㣬���ɵó��𰸣�
��3����3000�������ΪC��������ռ�İٷֱȣ��������һ���ο������ΪC��������
�⣺��1����D��֪��![]()
��ã�![]()
![]()
��2�����ΪB���ο�����Ӧ������Բ�ĽǵĶ����ǣ�360���0.4=144�㣻
��3����������ã� 3000��0.24=720��������
�𣺵���������һ���ο������ΪC������ԼΪ720����


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽԺʿ̸����������״��������ʱ˵����������Ҫ���ӷ�������Ҳ���ؿֻţ�������ȥ��Ա�ܼ��ij��������Ŵ����֣�������ע��ͨ�磬��ϴ�֣����˶����ٰ�ҹ.��ij����Ϊ�˼�ǿ�������������״����������֪ʶ���˽⣬ͨ����Ⱥ��������״�������ķ���֪ʶ�������������������߲�������![]() ������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�������
������״��������ȫ��ͳһ���ԣ�ȫ���������Ծ�������![]() �֣�����������Ա�������
�֣�����������Ա�������![]() �˵�ijС����ȡ��������Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�ͳ�������������һ����������ͳ�Ʊ�(��ͼ��ʾ)
�˵�ijС����ȡ��������Ա�Ĵ���ɼ����������ǵijɼ�����λ���֣�ͳ�������������һ����������ͳ�Ʊ�(��ͼ��ʾ)
�ȼ� | �ɼ�( | Ƶ�� | Ƶ�� |
|
|
| |
|
|
|
|
|
|
|
|
|
|
| |
�ϼ� |
|
| |
���������ṩ����Ϣ���ش��������⣺
��1��ͳ�Ʊ��е�![]() =___��
=___��![]() =_____��
=_____��
��2�����ݳ���������������Ƹ�С������ɼ�Ϊ��![]() �������ж����ˣ�
�������ж����ˣ�
��3����������![]() ���й���Ա��
���й���Ա��![]() ��Ů����Ա���ִ��������ѡ
��Ů����Ա���ִ��������ѡ![]() ������Ա�μӡ��������ء��������������״ͼ�����б������ǡ��ѡ�С�
������Ա�μӡ��������ء��������������״ͼ�����б������ǡ��ѡ�С�![]() ��
��![]() Ů���ĸ��ʣ�
Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����ڵ�![]() ��
��![]() ���������¶��壺
���������¶��壺
��� ����ô�Ƶ�
����ô�Ƶ�![]() Ϊ��
Ϊ��![]() �ġ�����㡱��
�ġ�����㡱��
���磺��![]() �ġ�����㡱Ϊ��
�ġ�����㡱Ϊ��![]() ����
����![]() �ġ�����㡱Ϊ��
�ġ�����㡱Ϊ��![]() ��
��
��1��ֱ��д����![]() �ġ�����㡱
�ġ�����㡱![]() �����꣮
�����꣮
��2����![]() �ں���
�ں���![]() ��ͼ���ϣ����䡰����㡱
��ͼ���ϣ����䡰����㡱![]() ��������Ϊ2������
��������Ϊ2������![]() �Ľ���ʽ��
�Ľ���ʽ��
��3����![]() �ں���
�ں���![]() ��ͼ���ϣ��ҵ�
��ͼ���ϣ��ҵ�![]() ����
����![]() ��Գƣ���
��Գƣ���![]() �ġ�����㡱Ϊ
�ġ�����㡱Ϊ![]() ������
������![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() �����ʱ������㡱
�����ʱ������㡱![]() �ĺ����꣮
�ĺ����꣮
��4����![]() �ں���
�ں���![]() ��ͼ���ϣ����䡰����㡱
��ͼ���ϣ����䡰����㡱![]() ��������
��������![]() �����ֵΪ
�����ֵΪ![]() ��ֱ��д��ʵ��
��ֱ��д��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A(-2��a)��C(3a-10��1)�Ƿ���������![]() ��x��0��ͼ���ϵ����㣮
��x��0��ͼ���ϵ����㣮
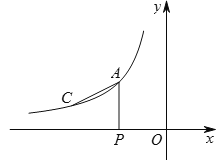
��1����m��ֵ��
��2������A��AP��x���ڵ�P����ֱ��y=kx+b������A������x�ύ�ڵ�B������PAC=��PABʱ����ֱ��AB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Եȱ���ABC�ı�BCΪֱ������O���ֱ�AB��AC�ڵ�D��E������D��DF��AC��AC�ڵ�F��
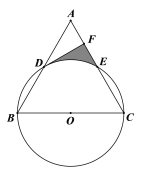
(1)��֤��DF�ǡ�O�����ߣ�
(2)���ȱ���ABC�ı߳�Ϊ8����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E�DZ�AD�ϵ�һ�㣬����CDE��CE�۵��õ���CFE����Fǡ�����ڱ�AB�ϣ�
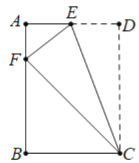
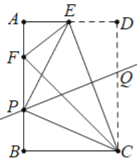
��1��֤������AEF�ס�BFC��
��2����AB=![]() ��BC=1�����߶�CE���д��ߣ���AB�ڵ�P����CD�ڵ�Q������PE��PC��
��BC=1�����߶�CE���д��ߣ���AB�ڵ�P����CD�ڵ�Q������PE��PC��
�����߶�DQ�ij���
�����жϡ�PCE����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽�ѧ�������ڼ�һ������ѧϰʱ����������һ������ʾ����飨ÿ��ֻ��ѡ������һ���������������������������������������ͳ��ͼ�������ͼ����Ϣ����������⣺
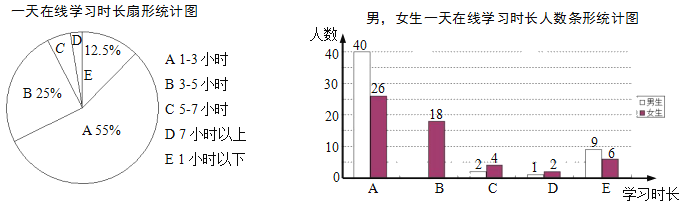
��1��������ʾ��������������
��2����ȫ����ͳ��ͼ�������һ������ѧϰ��5��7��Сʱ��������Բ�ĽǶ�����
��3������У����ѧ��1800�����Թ���ȫУһ������ѧϰ��7Сʱ���ϡ���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ���������˶��İ����ߣ������ֻ�������¼�������ڽ����ߵIJ�������λ���������Ƴ����µ�ͳ��ͼ�ٺ�ͳ��ͼ�ڣ�����������Ϣ������������⣺
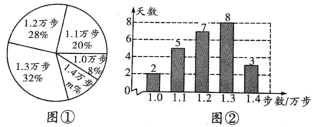
�����μ�¼��������Ϊ_____________��ͼ����m��ֵΪ______________��
������С�����ڽ����߲�����ƽ��������������λ����
�������������ݣ���С����ֽ�����һ�꣨��Ϊ365�죩���Թ��Ʋ���Ϊ1.1��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У�![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ����
����![]() ����
����![]() ��
��![]() ���ϵ�һ�����㣨���
���ϵ�һ�����㣨���![]() ��
��![]() ���غϣ�.ֱ��
���غϣ�.ֱ��![]() �Ǿ�����
�Ǿ�����![]() ��һ��ֱ�ߣ���
��һ��ֱ�ߣ���![]() ��ֱ��
��ֱ��![]() �۵�����
�۵�����![]() �Ķ�Ӧ���ǵ�
�Ķ�Ӧ���ǵ�![]() ��
��
��1����ͼ������![]() ʱ����ֱ��
ʱ����ֱ��![]() �����
�����![]() �����ꣻ
�����ꣻ
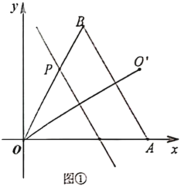
��2����ͼ��������![]() ��
��![]() �����˶�ʱ����ֱ��
�����˶�ʱ����ֱ��![]() ����
����![]() �������
�������
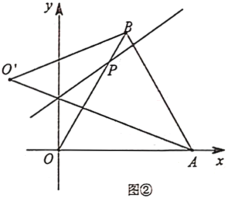
��3����![]() ʱ����ֱ��
ʱ����ֱ��![]() �仯�����У���
�仯�����У���![]() ��������ֵ��ֱ��д��������ɣ���
��������ֵ��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com