
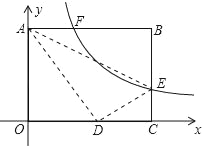
【题目】如图,矩形ABCO的顶点B(10,8),点A,C在坐标轴上,E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F,则线段BF的长为_____.
的图象与边AB交于点F,则线段BF的长为_____.
【答案】![]()
【解析】
首先根据翻折变换的性质,可得AD=AB=10,DE=BE;然后设点E的坐标是(10,b),在Rt△CDE中,根据勾股定理,求出CE的长度,进而求出k的值,再把F点的纵坐标代入解析式可求得F点的坐标,即可求得BF的长.
∵△ABE沿AE折叠,点B刚好与OC边上点D重合,
∴AD=AB=10,DE=BE,
∵AO=8,AD=10,
∴OD=![]() =6,
=6,
∴CD=10-6=4,
设点E的坐标是(10,b),
则CE=b,DE=10-b,
∵CD2+CE2=DE2,
∴42+b2=(8-b)2,
解得b=3,
∴点E的坐标是(10,3),
设反比例函数y=![]() ,
,
∴k=10×3=30,
∴反比例函数解析式为y=![]() ,
,
∵F点纵坐标为8,
∴8=![]() ,解得x=
,解得x=![]() ,即AF=
,即AF=![]() ,
,
∴BF=AB-AF=10-![]() =
=![]() ,
,
故答案为:![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某汽车制造厂生产一款电动汽车,计划一个月生产200辆.由于抽调不出足够的熟练工来完成电动汽车的安装,工厂决定招聘一些新工人,他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)若工厂现在有熟练工人30人,求还需要招聘多少新工人才能完成一个月的生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求
,求![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .
.
根据你的观察,探究下面的问题:
(1)已知![]() ,求
,求![]() 的值;
的值;
(2)已知△ABC的三边长![]() ,且满足
,且满足![]() ,求c的取值范围;
,求c的取值范围;
(3)已知![]() ,
,![]() ,比较
,比较![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
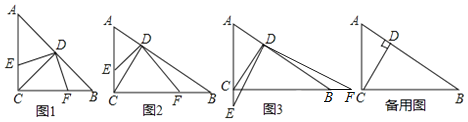
![]() 探究发现:
探究发现:
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
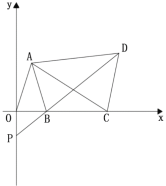
【题目】如图,平面直角坐标系中,已知点![]() 且
且![]() 为
为![]() 轴上点
轴上点![]() 右侧的动点,以
右侧的动点,以![]() 为腰作等腰
为腰作等腰![]() ,使
,使![]() 直线
直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当点![]() 运动时,点
运动时,点![]() 在
在![]() 轴上的位置是否发生改变,为什么?
轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第一象限,⊙A与x轴交于B(2,0)、C(8,0)两点,与y轴相切于点D,则点A的坐标是( )
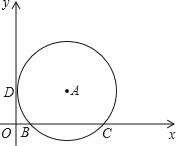
A. (5,4) B. (4,5) C. (5,3) D. (3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
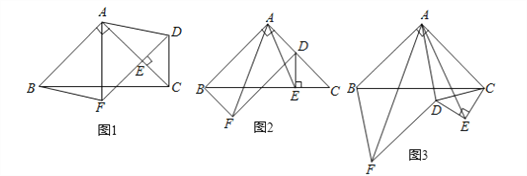
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com